
科目: 来源: 题型:
【题目】再直角坐标系中,定义两点![]() ,
,![]() 间的“直角距离”为
间的“直角距离”为![]() ,现有下列命题:
,现有下列命题:
①若![]() ,
,![]() 是
是![]() 轴上两点,则
轴上两点,则![]()
②已知![]() ,
,![]() ,则
,则![]() 为定值
为定值
③原点![]() 到直线
到直线![]() 上任一点
上任一点![]() 的直角距离
的直角距离![]() 的最小值为
的最小值为![]()
④设![]() 且
且![]() ,
,![]() ,若点
,若点![]() 是在过
是在过![]() 与
与![]() 的直线上,且点
的直线上,且点![]() 到点
到点![]() 与
与![]() 的“直角距离”之和等于
的“直角距离”之和等于![]() ,那么满足条件的点
,那么满足条件的点![]() 只有
只有![]() 个.
个.
其中的真命题是____________.(写出所有真命题的序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】某条公共汽车线路收支差额![]() 与乘客量
与乘客量![]() 的函数关系如下图所示(收支差额=车票收入-支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(1)不改变车票价格,减少支出费用;建议(2)不改变支出费用,提高车票价格.下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
的函数关系如下图所示(收支差额=车票收入-支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(1)不改变车票价格,减少支出费用;建议(2)不改变支出费用,提高车票价格.下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )

A.①反映建议(2),③反映建议(1)B.①反映建议(1),③反映建议(2)
C.②反映建议(1),④反映建议(2)D.④反映建议(1),②反映建议(2)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆锥的侧面展开图是一个半圆.

(1)求圆锥的母线与底面所成的角;
(2)过底面中心![]() 且平行于母线
且平行于母线![]() 的截平面,若截面与圆锥侧面的交线是焦参数(焦点到准线的距离)为
的截平面,若截面与圆锥侧面的交线是焦参数(焦点到准线的距离)为![]() 的抛物线,求圆锥的全面积;
的抛物线,求圆锥的全面积;
(3)过底面点![]() 作垂直且于母线
作垂直且于母线![]() 的截面,若截面与圆锥侧面的交线是长轴为
的截面,若截面与圆锥侧面的交线是长轴为![]() 的椭圆,求椭圆的面积(椭圆号
的椭圆,求椭圆的面积(椭圆号![]() 的面积
的面积![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在底面是菱形的四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
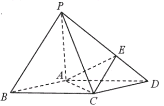
(1)证明:![]() 面
面![]() ;
;
(2)在棱![]() 上是否存在一点
上是否存在一点![]() ,使三棱锥
,使三棱锥![]() 是正三棱锥?证明你的结论.
是正三棱锥?证明你的结论.
(3)求以![]() 为棱,
为棱,![]() 与
与![]() 为面的二面角
为面的二面角![]() 的大小.
的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,![]() .
.
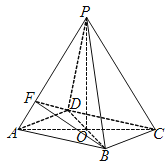
(1)求四棱锥P-ABCD的体积VP-ABCD;
(2)在线段PB上是否存在一点M,使得CM∥平面BDF?如果存在,求![]() 的值,如果不存在,请说明理由.
的值,如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正四棱柱![]() ,中,
,中,![]() .
.

(1)求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)若![]() 是线段
是线段![]() 上(不含线段的两端点)的一个动点,请提出一个与三棱锥体积有关的数学问题(注:三棱锥需以点
上(不含线段的两端点)的一个动点,请提出一个与三棱锥体积有关的数学问题(注:三棱锥需以点![]() 和已知正四棱柱八个顶点中的三个为顶点构成);并解答所提出的问题.
和已知正四棱柱八个顶点中的三个为顶点构成);并解答所提出的问题.
查看答案和解析>>
科目: 来源: 题型:
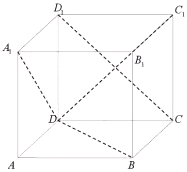
【题目】如图,![]() 的棱长为1的正方体,任作平面
的棱长为1的正方体,任作平面![]() 与对角线
与对角线![]() 垂直,使得
垂直,使得![]() 与正方体的每个面都有公共点,这样得到的截面多边形的面积为
与正方体的每个面都有公共点,这样得到的截面多边形的面积为![]() ,周长为
,周长为![]() 的范围分别是_____________(用集合表示)
的范围分别是_____________(用集合表示)
查看答案和解析>>
科目: 来源: 题型:
【题目】国家环境标准制定的空气质量指数与空气质量等级对应关系如表:
空气质量指数 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | 300以上 |
空气质量等级 | 1级优 | 2级良 | 3级轻 度污染 | 4级中度污染 | 5级重 度污染 | 6级严重污染 |
由全国重点城市环境监测网获得10月份某五天甲城市和乙城市的空气质量指数数据用茎叶图表示如图:
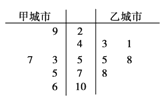
(1)试根据上面的统计数据,计算甲、乙两个城市的空气质量指数的方差;
(2)试根据上面的统计数据,估计甲城市某一天空气质量等级为2级良的概率;
(3)分别从甲城市和乙城市的统计数据中任取一个,试求两个城市空气质量等级相同的概率.供参考数据:292+532+572+752+1062=23760,432+412+552+582+782=16003
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com