
科目: 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
以平面直角坐标系xOy的原点为极点,x轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线l的坐标方程为![]() ,曲线C的参数方程为
,曲线C的参数方程为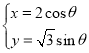 (θ为参数).
(θ为参数).
(1)求直线l的直角坐标方程和曲线C的普通方程;
(2)以曲线C上的动点M为圆心、r为半径的圆恰与直线l相切,求r的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】众所周知的“太极图”,其形状如对称的阴阳两鱼互抱在一起,因而也被称为“阴阳鱼太极图”.如图是放在平面直角坐标系中的“太极图”,整个图形是一个圆形,其中黑色阴影区域在![]() 轴右侧部分的边界为一个半圆.给出以下命题:①在太极图中随机取一点,此点取自黑色阴影部分的概率是
轴右侧部分的边界为一个半圆.给出以下命题:①在太极图中随机取一点,此点取自黑色阴影部分的概率是![]() ;②当
;②当![]() 时,直线
时,直线![]() 与黑色阴影部分有公共点;③当
与黑色阴影部分有公共点;③当![]() 时,直线
时,直线![]() 与黑色阴影部分有两个公共点.其中所有正确结论的序号是( )
与黑色阴影部分有两个公共点.其中所有正确结论的序号是( )
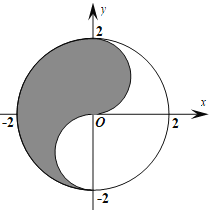
A.①B.①②C.①③D.①②③
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,短轴长为![]() ,离心率为
,离心率为![]() .
.
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程;
求椭圆C的方程;
![]() Ⅱ
Ⅱ![]() 若过点
若过点![]() 的直线与椭圆C交于A,B两点,且P点平分线段AB,求直线AB的方程;
的直线与椭圆C交于A,B两点,且P点平分线段AB,求直线AB的方程;
![]() Ⅲ
Ⅲ![]() 一条动直线l与椭圆C交于不同两点M,N,O为坐标原点,
一条动直线l与椭圆C交于不同两点M,N,O为坐标原点,![]() 的面积为
的面积为![]() 求证:
求证:![]() 为定值.
为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中,![]() 底面ABC,
底面ABC,![]() 点D,E分别为棱PA,PC的中点,M是线段AD的中点,N是线段BC的中点,
点D,E分别为棱PA,PC的中点,M是线段AD的中点,N是线段BC的中点,![]() ,
,![]() .
.

![]() Ⅰ
Ⅰ![]() 求证:
求证:![]() 平面BDE;
平面BDE;
![]() Ⅱ
Ⅱ![]() 求直线MN到平面BDE的距离;
求直线MN到平面BDE的距离;
![]() Ⅲ
Ⅲ![]() 求二面角
求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=ax+lnx(a∈R),g(x)=x2emx(m∈R,e为自然对数的底数).
(1)讨论函数f(x)的单调性及最值;
(2)若a>0,且对x1,x2∈[0,2],f(x1+1)≥g(x2)+a﹣1恒成立,求实数m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】圆O:x2+y2=9上的动点P在x轴、y轴上的射影分别是P1,P2,点M满足![]() .
.
(1)求点M的轨迹C的方程;
(2)点A(0,1),B(0,﹣3),过点B的直线与轨迹C交于点S,N,且直线AS、AN的斜率kAS,kAN存在,求证:kASkAN为常数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1(侧棱垂直于底面的棱柱)中,CA⊥CB,CA=CB=CC1=2,动点D在线段AB上.
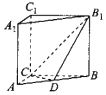
(1)求证:当点D为AB的中点时,平面B1CD⊥上平面ABB1A1;
(2)当AB=3AD时,求平面B1CD与平面BB1C1C所成的锐二面角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学高一期中考试结束后,从高一年级1000名学生中任意抽取50名学生,将这50名学生的某一科的考试成绩(满分150分)作为样本进行统计,并作出样本成绩的频率分布直方图(如图).
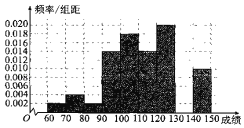
(1)由于工作疏忽,将成绩[130,140)的数据丢失,求此区间的人数及频率分布直方图的中位数;(结果保留两位小数)
(2)若规定考试分数不小于120分为优秀,现从样本的优秀学生中任意选出3名学生,参加学习经验交流会.设X表示参加学习经验交流会的学生分数不小于130分的学生人数,求X的分布列及期望;
(3)视样本频率为概率.由于特殊原因,有一个学生不能到学校参加考试,根据以往考试成绩,一般这名学生的成绩应在平均分左右.试根据以上数据,说明他若参加考试,可能得多少分?(每组数据以区问的中点值为代表)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com