
科目: 来源: 题型:
【题目】设A是圆O:x2+y2=16上的任意一点,l是过点A且与x轴垂直的直线,B是直线l与x轴的交点,点Q在直线l上,且满足4|BQ|=3|BA|.当点A在圆O上运动时,记点Q的轨迹为曲线C.
(1)求曲线C的方程;
(2)已知直线y=kx﹣2(k≠0)与曲线C交于M,N两点,点M关于y轴的对称点为M′,设P(0,﹣2),证明:直线M′N过定点,并求△PM′N面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,已知曲线![]() ,以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:p(2cosθ-sinθ)=6.
,以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:p(2cosθ-sinθ)=6.
(1)试写出直线l的直角坐标方程和曲线C1的参数方程;
(2)在子曲线C1上求一点P,使点P到直线l的距离最大,并求出此最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆C:x2+y2+2x﹣2y+1=0和抛物线E:y2=2px(p>0),圆C与抛物线E的准线交于M、N两点,△MNF的面积为p,其中F是E的焦点.
(1)求抛物线E的方程;
(2)不过原点O的动直线l交该抛物线于A,B两点,且满足OA⊥OB,设点Q为圆C上任意一动点,求当动点Q到直线l的距离最大时直线l的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了促进学生的全面发展,某市教育局要求本市所有学校重视社团文化建设,2014年该市某中学的某新生想通过考核选拨进入该校的“电影社”和“心理社”,已知该同学通过考核选拨进入这两个社团成功与否相互独立根据报名情况和他本人的才艺能力,两个社团都能进入的概率为![]() ,至少进入一个社团的概率为
,至少进入一个社团的概率为![]() ,并且进入“电影社”的概率小于进入“心理社”的概率
,并且进入“电影社”的概率小于进入“心理社”的概率
(Ⅰ)求该同学分别通过选拨进入“电影社”的概率![]() 和进入心理社的概率
和进入心理社的概率![]() ;
;
(Ⅱ)学校根据这两个社团的活动安排情况,对进入“电影社”的同学增加1个校本选修课学分,对进入“心理社”的同学增加0.5个校本选修课学分.求该同学在社团方面获得校本选修课学分分数不低于1分的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点A(1,0),圆E:(x+1)2+y2=16,点B是圆E上任意一点,线段AB的垂直平分线l与半径EB相交于H.
(1)当点B在圆上运动时,求动点H的轨迹г的方程:
(2)过点A且与坐标轴不垂直的直线交轨迹г于![]() 、
、![]() 两点,线段OA(O为坐标原点)上是否存在点
两点,线段OA(O为坐标原点)上是否存在点![]() 使得
使得![]() 若存在,求出实数m的取值范围;若不存在,说明理由.
若存在,求出实数m的取值范围;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,已知棱锥P-ABC 中.PA⊥平面ABC,AB⊥AC,PA=AC=![]() AB=1,N为AB 上一点,AB=4AN,M.S分别为PB,BC的中点.
AB=1,N为AB 上一点,AB=4AN,M.S分别为PB,BC的中点.
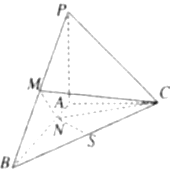
(1)证明:CM⊥SN;
(2)求二面角M-NC-B的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com