
科目: 来源: 题型:
【题目】某互联网公司为了确定下一季度的前期广告投入计划,收集了近![]() 个月广告投入量
个月广告投入量![]() (单位:万元)和收益
(单位:万元)和收益![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
月份 |
|
|
|
|
|
|
广告投入量 |
|
|
|
|
|
|
收益 |
|
|
|
|
|
|
他们分别用两种模型①![]() ,②
,②![]() 分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
|
|
|
|
|
|
|
|

(Ⅰ)根据残差图,比较模型①,②的拟合效果,应选择哪个模型?并说明理由;
(Ⅱ)残差绝对值大于![]() 的数据被认为是异常数据,需要剔除:
的数据被认为是异常数据,需要剔除:
(ⅰ)剔除异常数据后求出(Ⅰ)中所选模型的回归方程
(ⅱ)若广告投入量![]() 时,该模型收益的预报值是多少?
时,该模型收益的预报值是多少?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
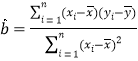
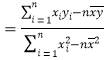 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男 | 女 | 合计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
合计 | 60 | 50 | 110 |
由K2=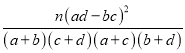 ,
,
附表:
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() 且
且![]() .
.
(1)求实数![]() 的值;
的值;
(2)判断函数![]() 在区间
在区间![]() 上的单调性,并用函数单调性的定义证明;
上的单调性,并用函数单调性的定义证明;
(3)求实数![]() 的取值范围,使得关于
的取值范围,使得关于![]() 的方程
的方程![]() 分别为:
分别为:
①有且仅有一个实数解;②有两个不同的实数解;③有三个不同的实数解.
查看答案和解析>>
科目: 来源: 题型:
【题目】设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .数列
.数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)写出一个正整数![]() ,使得
,使得![]() 是数列
是数列![]() 的项;
的项;
(3)设数列![]() 的通项公式为
的通项公式为![]() ,问:是否存在正整数
,问:是否存在正整数![]() 和
和![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差数列?若存在,请求出所有符合条件的有序整数对
成等差数列?若存在,请求出所有符合条件的有序整数对![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知A(4,0)、B(1,0),动点M满足|AM|=2|BM|.
(1)求动点M的轨迹C的方程;
(2)直线l:x+y=4,点N∈l,过N作轨迹C的切线,切点为T,求NT取最小时的切线方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】设定义在![]() 上的函数
上的函数![]() 满足:对任意的
满足:对任意的![]() ,当
,当![]() 时,都有
时,都有![]() .
.
(1)若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 为周期函数,证明:
为周期函数,证明:![]() 是常值函数;
是常值函数;
(3)若![]() 在
在![]() 上满足:
上满足:![]() ,
,![]() ,
,![]() ,
,
①记![]() (
(![]() ),求数列
),求数列![]() 的通项公式;② 求
的通项公式;② 求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (
(![]() ),数列
),数列![]() 满足
满足![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() .
.
(1)求证:数列![]() 是等差数列;
是等差数列;
(2)设数列![]() 满足
满足![]() (
(![]() ),且
),且![]() 中任意连续三项均能构成一个三角形的三边长,求
中任意连续三项均能构成一个三角形的三边长,求![]() 的取值范围;
的取值范围;
(3)设数列![]() 满足
满足![]() (
(![]() ),求
),求![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知A(4,0)、B(1,0),动点M满足|AM|=2|BM|.
(1)求动点M的轨迹C的方程;
(2)直线l:x+y=4,点N∈l,过N作轨迹C的切线,切点为T,求NT取最小时的切线方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知动点M到定点F1(-2,0)和F2(2,0)的距离之和为![]() .
.
(1)求动点M的轨迹C的方程;
(2)设N(0,2),过点P(-1,-2)作直线l,交曲线C于不同于N的两点A,B,直线NA,NB的斜率分别为k1,k2,求k1+k2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com