
科目: 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点
的左、右焦点![]() ,
,![]() ,
,![]() 是椭圆
是椭圆![]() 上的动点,且
上的动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程及离心率;
的方程及离心率;
(2)若![]() 是椭圆
是椭圆![]() 的左、右顶点,直线
的左、右顶点,直线![]() 与椭圆在点
与椭圆在点![]() 处的切线交于点
处的切线交于点![]() ,当点
,当点![]() 在椭圆上运动时,求证:以
在椭圆上运动时,求证:以![]() 为直径的圆与直线
为直径的圆与直线![]() 恒相切.
恒相切.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() 是圆
是圆![]() :
:![]() 上的一动点,点
上的一动点,点![]() ,点
,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设曲线![]() 与
与![]() 轴的正半轴,
轴的正半轴,![]() 轴的正半轴的交点分别为点
轴的正半轴的交点分别为点![]() ,
,![]() ,斜率为
,斜率为![]() 的动直线
的动直线![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点,其中点
两点,其中点![]() 在第一象限,求四边形
在第一象限,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】近年来,随着互联网技术的快速发展,共享经济覆盖的范围迅速扩张,继共享单车、共享汽车之后,共享房屋以“民宿”、“农家乐”等形式开始在很多平台上线.某创业者计划在某景区附近租赁一套农房发展成特色“农家乐”,为了确定未来发展方向,此创业者对该景区附近六家“农家乐”跟踪调查了![]() 天.得到的统计数据如下表,
天.得到的统计数据如下表,![]() 为收费标准(单位:元/日),
为收费标准(单位:元/日),![]() 为入住天数(单位:),以频率作为各自的“入住率”,收费标准
为入住天数(单位:),以频率作为各自的“入住率”,收费标准![]() 与“入住率”
与“入住率”![]() 的散点图如图
的散点图如图
x | 50 | 100 | 150 | 200 | 300 | 400 |
t | 90 | 65 | 45 | 30 | 20 | 20 |
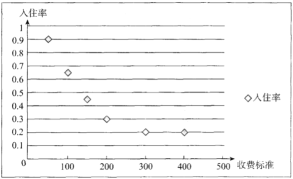
(1)若从以上六家“农家乐”中随机抽取两家深入调查,记![]() 为“入住率”超过
为“入住率”超过![]() 的农家乐的个数,求
的农家乐的个数,求![]() 的概率分布列;
的概率分布列;
(2)令![]() ,由散点图判断
,由散点图判断![]() 与
与![]() 哪个更合适于此模型(给出判断即可,不必说明理由)?并根据你的判断结果求回归方程.(
哪个更合适于此模型(给出判断即可,不必说明理由)?并根据你的判断结果求回归方程.(![]() 结果保留一位小数)
结果保留一位小数)
(3)若一年按![]() 天计算,试估计收费标准为多少时,年销售额
天计算,试估计收费标准为多少时,年销售额![]()
![]() 入住率
入住率![]() 收费标准
收费标准![]() )
)
参考数据: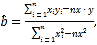
![]()
![]()
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】甲袋中装有2个白球,3个黑球,乙袋中装有1个白球,2个黑球,这些球除颜色外完全相同.
(1)从两袋中各取1个球,记事件![]() :取出的2个球均为白球,求
:取出的2个球均为白球,求![]() ;
;
(2)每次从甲、乙两袋中各取2个球,若取出的白球不少于2个就获奖(每次取完后将球放回原袋),共取了3次,记获奖次数为![]() ,写出
,写出![]() 的分布列并求
的分布列并求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲和乙两个人计划周末参加志愿者活动,约定在周日早上8:00至8:30之间到某公交站搭乘公交车一起去,已知在这段时间内,共有![]() 班公交车到达该站,到站的时间分别为8:05,8:15,8:30,如果他们约定见车就搭乘,则甲和乙两个人恰好能搭乘同一班公交车去的概率为( )
班公交车到达该站,到站的时间分别为8:05,8:15,8:30,如果他们约定见车就搭乘,则甲和乙两个人恰好能搭乘同一班公交车去的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,现有4种不同颜色给图中5个区域涂色,要求任意两个相邻区域不同色,共有______种不同涂色方法;若要求4种颜色都用上且任意两个相邻区域不同色,共有______种不同涂色方法.(用数字作答)
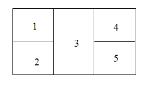
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com