
科目: 来源: 题型:
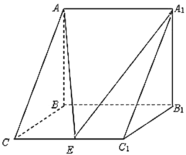
【题目】如图,三棱柱![]() 中,
中,![]() 侧面
侧面![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,点
,点![]() 是棱
是棱![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,
,![]() 分别为双曲线
分别为双曲线![]()
![]()
![]() 的左、右焦点,点P是以
的左、右焦点,点P是以![]() 为直径的圆与C在第一象限内的交点,若线段
为直径的圆与C在第一象限内的交点,若线段![]() 的中点Q在C的渐近线上,则C的两条渐近线方程为__________.
的中点Q在C的渐近线上,则C的两条渐近线方程为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,已知圆
中,已知圆![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() :
:![]() 与圆
与圆![]() 的交点为
的交点为![]() 、
、![]() 两点,
两点,![]() 与直线
与直线![]() 的交点为
的交点为![]() .
.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)求线段![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】设抛物线C:![]() 与直线
与直线![]() 交于A、B两点.
交于A、B两点.
(1)当![]() 取得最小值为
取得最小值为![]() 时,求
时,求![]() 的值.
的值.
(2)在(1)的条件下,过点![]() 作两条直线PM、PN分别交抛物线C于M、N(M、N不同于点P)两点,且
作两条直线PM、PN分别交抛物线C于M、N(M、N不同于点P)两点,且![]() 的平分线与
的平分线与![]() 轴平行,求证:直线MN的斜率为定值.
轴平行,求证:直线MN的斜率为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校在高一部分学生中调查男女同学对某项体育运动的喜好情况,其二维条形图如图(黑色代表喜好,白色代表不喜好).
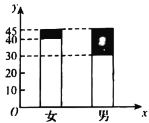
(1)写出![]() 列联表;
列联表;
(2)能否有99%的把握认为喜好这项体育运动与性别有关;
(3)在这次调查中从喜好这项体育活动的一名男生和两名女生中任选两人进行专业培训,求恰是一男一女的概率.
附: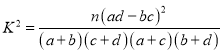
| 0.25 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目: 来源: 题型:
【题目】自新型冠状病毒疫情爆发以来,人们时刻关注疫情,特别是治愈率,治愈率![]() 累计治愈人数/累计确诊人数,治愈率的高低是“战役”的重要数据,由于确诊和治愈人数在不断变化,那么人们就非常关心第
累计治愈人数/累计确诊人数,治愈率的高低是“战役”的重要数据,由于确诊和治愈人数在不断变化,那么人们就非常关心第![]() 天的治愈率,以此与之前的治愈率比较,来推断在这次“战役”中是否有了更加有效的手段,下面是一段计算治愈率的程序框图,请同学们选出正确的选项,分别填入①②两处,完成程序框图.( )
天的治愈率,以此与之前的治愈率比较,来推断在这次“战役”中是否有了更加有效的手段,下面是一段计算治愈率的程序框图,请同学们选出正确的选项,分别填入①②两处,完成程序框图.( )
![]() :第
:第![]() 天新增确诊人数;
天新增确诊人数;![]() :第
:第![]() 天新增治愈人数;
天新增治愈人数;![]() :第
:第![]() 天治愈率
天治愈率
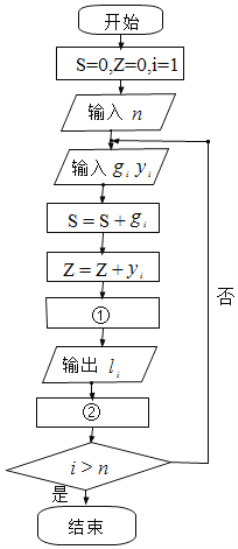
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】给出下列四个结论:
①若![]() 在
在![]() 上是奇函数,则
上是奇函数,则![]() 在
在![]() 上也是奇函数
上也是奇函数
②若![]() 不是正弦函数,则
不是正弦函数,则![]() 不是周期函数
不是周期函数
③“若![]() ,则
,则![]() .”的否命题是“若
.”的否命题是“若![]() ,则
,则![]() .”
.”
④若![]() :
:![]() ;
;![]() :
:![]() ,则
,则![]() 是
是![]() 的充分不必要条件
的充分不必要条件
其中正确结论的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,已知圆
中,已知圆![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() :
:![]() 与圆
与圆![]() 的交点为
的交点为![]() 、
、![]() 两点,
两点,![]() 与直线
与直线![]() 的交点为
的交点为![]() .
.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com