【题目】在直角坐标系中，以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为．

（1）为曲线上的动点，点在线段上，且满足，求点的轨迹的直角坐标方程；

（2）设点的极坐标为，点在曲线上，求面积的最大值．

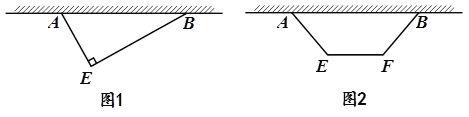
方案① 多边形为直角三角形（），如图1所示，其中；

方案② 多边形为等腰梯形（），如图2所示，其中．

请你分别求出两种方案中苗圃的最大面积，并从中确定使苗圃面积最大的方案．

(1) 求证：BC⊥平面VCD；

(2) 求证：AD∥MN.

【题目】已知函数有两个零点，且

（1）求的取值范围；

（2）证明：随着的增大而减小；

（3）证明：随着的增大而减小.

【题目】在平面直角坐标系xOy中,已知椭圆C: (a>b>0)的离心率为,椭圆C截直线y=1所得线段的长度为.

(Ⅰ)求椭圆C的方程；

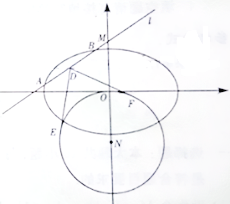
(Ⅱ)动直线l:y=kx+m(m≠0)交椭圆C于A,B两点,交y轴于点M.点N是M关于O的对称点,⊙N的半径为|NO|. 设D为AB的中点,DE,DF与⊙N分别相切于点E,F,求EDF的最小值.

其中每一级过滤都由核心部件滤芯来实现。在使用过程中，一级滤芯和二级滤芯都需要不定期更换（每个滤芯是否需要更换相互独立），三级滤芯无需更换，若客户在安装净水系统的同时购买滤芯，则一级滤芯每个元，二级滤芯每个元.若客户在使用过程中单独购买滤芯，则一级滤芯每个元，二级滤芯每个元。现需决策安装净水系统的同时购滤芯的数量，为此参考了根据套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表，其中图是根据个一级过滤器更换的滤芯个数制成的柱状图，表是根据个二级过滤器更换的滤芯个数制成的频数分布表.

二级滤芯更换频数分布表

以个一级过滤器更换滤芯的频率代替个一级过滤器更换滤芯发生的概率，以个二级过滤器更换滤芯的频率代替个二级过滤器更换滤芯发生的概率.

（1）求一套净水系统在使用期内需要更换的各级滤芯总个数恰好为的概率；

（2）记表示该客户的净水系统在使用期内需要更换的一级滤芯总数，求的分布列及数学期望；

（3）记，分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若，且，以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据，试确定，的值.

(1)求证：AB∥FG；

(2)若PA⊥底面ABCDE，且PA＝AE.求直线BC与平面ABF所成角的大小，并求线段PH的长．

【题目】平面上到两个定点的距离的积为定值的动点轨迹一般称为卡西尼（cassin）卵形线，已知曲线为到定点的距离之积为常数4的点的轨迹，关于曲线的几何性质有下四个结论，其中错误的是（ ）

A.曲线关于原点对称B.的面积的最大值为2

C.其中的取值范围为D.其中的取值范围为

【题目】为了解户籍性别对生育二胎选择倾向的影响，某地从育龄人群中随机抽取了容量为的调查样本，其中城镇户籍与农民户籍各人；男性人，女性人.绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图（如图所示），其中阴影部分表示倾向选择生育二胎的对应比例，则下列叙述中错误的是（ ）

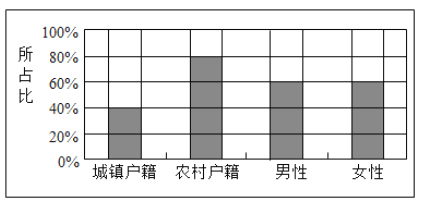
A.是否倾向选择生育二胎与户籍有关

B.是否倾向选择生育二胎与性别无关

C.倾向选择生育二胎的人员中，男性人数与女性人数相同

D.倾向选择不生育二胎的人员中，农村户籍人数少于城镇户籍人数