【题目】九章算术是我国古代著名数学经典其中对勾股定理的论述比西方早一千多年，其中有这样一个问题：“今有圆材埋在壁中，不知大小以锯锯之，深一寸，锯道长一尺问径几何？”其意为：今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯该材料，锯口深一寸，锯道长一尺问这块圆柱形木料的直径是多少？长为1丈的圆柱形木材部分镶嵌在墙体中，截面图如图所示阴影部分为镶嵌在墙体内的部分已知弦尺，弓形高寸，估算该木材镶嵌在墙中的体积约为( )(注：1丈尺寸，，)

A. 600立方寸 B. 610立方寸 C. 620立方寸 D. 633立方寸

【题目】已知，．

（1）如果函数的单调递减区间为，求函数的解析式；

（2）在（1）的条件下，求函数的图象在点处的切线方程；

（3）若不等式恒成立，求实数a的取值范围．

【题目】将函数的图像向左平移个单位长度，再将图像上所有点的横坐标伸长到原来的倍（纵坐标不变），得到的图像.

（1）求的单调递增区间；

（2）若对于任意的，不等式恒成立，求实数的取值范围.

（1）求f（x）的表达式；

（2）若f（x）＞a在x∈[﹣1，1]恒成立，求实数a的取值范围．

【题目】已知函数.

(1)讨论的单调性；

(2)若有两个极值点，不等式恒成立，求实数的取值范围.

【题目】随着创新驱动发展战略的不断深入实施，高新技术企业在科技创新和经济发展中的带动作用日益凸显，某能源科学技术开发中心拟投资开发某新型能源产品，估计能获得万元的投资收益，现准备制定一个对科研课题组的奖励议案：奖金（单位：万元）随投资收益（单位：万元）的增加而增加，奖金不超过万元，同时奖金不超过投资收益的.（即：设奖励方案函数模拟为时，则公司对函数模型的基本要求是：当时，①是增函数；②恒成立；③恒成立.）

（1）现有两个奖励函数模型：（I）；（II）.试分析这两个函数模型是否符合公司要求？

（2）已知函数符合公司奖励方案函数模型要求，求实数的取值范围.

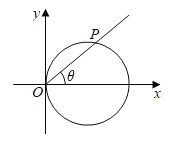
【题目】（1）如图，以过原点的直线的倾斜角为参数，求圆的参数方程；

（2）在平面直角坐标系中，已知直线的参数方程为，（为参数），曲线的参数方程为（为参数），若与相交于两点，求的长.

（I）讨论f(x)的单调性；

（II）确定a的所有可能取值，使得在区间（1，+∞）内恒成立(e=2.718…为自然对数的底数)。

【题目】如图，已知抛物线.点A，抛物线上的点P（x,y）,过点B作直线AP的垂线，垂足为Q

（I）求直线AP斜率的取值范围；

（II）求的最大值

（1）写出数表的第六行（从左至右依次列出）．

（2）设第n行的第二个数为bn（n≥2），求bn．

（3）令，记Tn为数列前n项和，求的最大值，并求此时n的值．