【题目】新型冠状病毒肺炎是一种急性感染性肺炎，其病原体是一种先前未在人类中发现的新型冠状病毒，即2019新型冠状病毒.2020年2月7日，国家卫健委决定将“新型冠状病毒感染的肺炎”暂命名为“新型冠状病毒肺炎”，简称“新冠肺炎”.患者初始症状多为发热、乏力和干咳，并逐渐出现呼吸困难等严重表现.基于目前流行病学调查，潜伏期为1~14天，潜伏期具有传染性，无症状感染者也可能成为传染源.某市为了增强民众防控病毒的意识，举行了“预防新冠病毒知识竞赛”网上答题，随机抽取人，答题成绩统计如图所示.

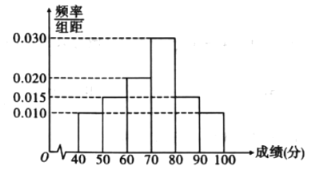
（1）由直方图可认为答题者的成绩服从正态分布，其中分别为答题者的平均成绩和成绩的方差，那么这名答题者成绩超过分的人数估计有多少人？（同一组中的数据用该组的区间中点值作代表）

（2）如果成绩超过分的民众我们认为是“防御知识合格者”，用这名答题者的成绩来估计全市的民众，现从全市中随机抽取人，“防御知识合格者”的人数为，求.（精确到）

附：①，；②，则，；③，.

【题目】已知函数.

（1）证明：；

（2）（i）证明：当时，对任意，总有；

（ii）讨论函数的零点个数.

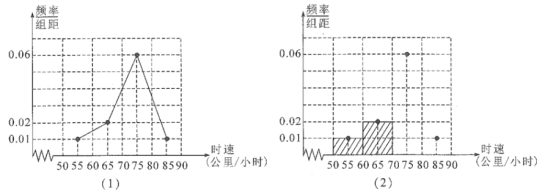
（1）请根据频率分布折线图，将颊率分布直方图补充完整（用阴影部分表示）；

（2）求这200辆汽车在该路段超速的车辆数以及在该路段的平均速度.

①与②与

③与④与

则“互为镜像方程对”的是（ ）

A.①②③B.①③④C.②③④D.①②③④

【题目】如图所示，椭圆的离心率为，过点作直线交椭圆于不同两点，．

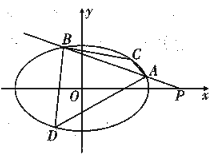
（1）求椭园的方程；

（2）①设直线的斜率为，求出与直线平行且与椭圆相切的直线方程（用表示）；

②若，为椭圆上的动点，求四边形面积的最大值．

【题目】已知函数.

（1）求的单调区间与极值；

（2）当函数有两个极值点时，求实数a的取值范围.

【题目】已知三棱锥的四个顶点都在球的表面上，平面，，，，，则球的半径为______；若是的中点，过点作球的截面，则截面面积的最小值是______．

【题目】从2020年起，北京考生的高考成绩由语文、数学、外语3门统一高考成绩和考生选考的3门普通高中学业水平考试等级性考试科目成绩构成．等级性考试成绩位次由高到低分为，，，，，各等级人数所占比例依次为：等级15%，等级40%，等级30%，等级14%，等级1%．现采用分层抽样的方法，从参加历史等级性考试的学生中抽取1000人作为样本，则该样本中获得或等级的学生人数为（ ）

A.275B.400C.550D.450

【题目】已知椭圆过点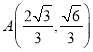，其左、右两个焦点分别为，，短轴的一个端点为，且.

（1）求的平分线所在的直线方程；

（2）设直线：与椭圆交于不同的两点，.且为坐标原点，若，求的面积的最大值.

（1）应从甲、乙、丙三个部门的员工中分别抽取多少人？

（2）若抽出的7人中有3人是抖音迷，4人为非抖音迷，现从这7人中随机抽取3人做进一步的详细登记．

①用表示抽取的3人中是抖音迷的员工人数，求随机变量的分布列与数学期望；

②设为事件“抽取的3人中，既有是抖音迷的员工，也有非抖音迷的员工’’，求事件发生的概率．