该蛋糕店一天制作了这款蛋糕X（X∈N）个，以x（单位：个，100≤x≤150，x∈N）表示当天的市场需求量，T（单位：元）表示当天出售这款蛋糕获得的利润．

（1）当x＝135时，若X＝130时获得的利润为T1，X＝140时获得的利润为T2，试比较T1和T2的大小；

（2）当X＝130时，根据上表，从利润T不少于560元的天数中，按需求量分层抽样抽取6天．

（i）求此时利润T关于市场需求量x的函数解析式，并求这6天中利润为650元的天数；

（ii）再从这6天中抽取3天做进一步分析，设这3天中利润为650元的天数为ξ，求随机变量ξ的分布列及数学期望．

（1）设直线AF，BF的斜率分別为k1，k2，证明：k1+k2＝0；

（2）若的面积为，求直线l的方程．

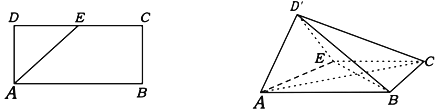
（1）求证：平面ABD'⊥平面BD'E；

（2）求直线CE与平面BCD'所成角的正弦值．

【题目】已知函数．

（1）求函数f（x）在[0，π]上的单调递减区间；

（2）在锐角△ABC的内角A，B，C所对边为a，b，c，已知f（A）＝﹣1，a＝2，求△ABC的面积的最大值．

A.（0，1）B.C.（1，+∞）D.

①“x＞1”是“x＞2”的充分不必要条件；

②f（x）是其定义域上的可导函数，“f'（x0）＝0”是“y＝f（x）在x0处有极值”的充要条件；

③命题“若a＞b，则2a＞2b﹣1”的否命题为“若a≤b，则2a≤2b﹣1”；

④若“p且q”为假命题，则p、q均为假命题．

A.1B.2C.3D.4

【题目】一种新的验血技术可以提高血液检测效率.现某专业检测机构提取了份血液样本，其中只有1份呈阳性，并设计了如下混合检测方案：先随机对其中份血液样本分别取样，然后再混合在一起进行检测，若检测结果为阴性，则对另外3份血液逐一检测，直到确定呈阳性的血液为止；若检测结果呈阳性，测对这份血液再逐一检测，直到确定呈阳性的血液为止.

（1）若，求恰好经过3次检测而确定呈阳性的血液的事件概率；

（2）若，宜采用以上方案检测而确定呈阳性的血液所需次数为，

①求的概率分布；

②求.

【题目】对于，若数列满足，则称这个数列为“K数列”．

（Ⅰ）已知数列：1，m+1，m2是“K数列”，求实数的取值范围；

（Ⅱ）是否存在首项为-1的等差数列为“K数列”，且其前n项和满足

？若存在，求出的通项公式；若不存在，请说明理由；

（Ⅲ）已知各项均为正整数的等比数列是“K数列”，数列不是“K数列”，若，试判断数列是否为“K数列”，并说明理由．

【题目】设函数，

（1）当时，求函数图象在处的切线方程；

（2）求的单调区间；

（3）若不等式对恒成立，求整数的最大值.

【题目】如图所示，某区有一块空地，其中，，.当地区政府规划将这块空地改造成一个旅游景点，拟在中间挖一个人工湖，其中都在边上，且，挖出的泥土堆放在地带上形成假山，剩下的地带开设儿童游乐场.为安全起见，需在的周围安装防护网.

（1）当时，求防护网的总长度；

（2）若要求挖人工湖用地的面积是堆假山用地的面积的倍，试确定的大小；

（3）为节省投入资金，人工湖的面积要尽可能小，问如何设计施工方案，可使的面积最小？最小面积是多少？