【题目】在平面直角坐标系中，直线的参数方程为（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为．

（Ⅰ）求直线的普通方程和曲线的直角坐标方程；

（Ⅱ）设为曲线上的点，，垂足为，若的最小值为，求的值．

【题目】设函数，，．

（1）讨论函数的单调性；

（2）若（其中），证明：；

（3）是否存在实数a，使得在区间内恒成立，且关于x的方程在内有唯一解？请说明理由．

【题目】如图是一“T”型水渠的平面视图（俯视图），水渠的南北方向和东西方向轴截面均为矩形，南北向渠宽为4m，东西向渠宽m（从拐角处，即图中，处开始）．假定渠内的水面始终保持水平位置（即无高度差）．

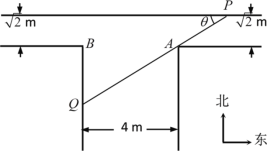
（1）在水平面内，过点的一条直线与水渠的内壁交于，两点，且与水渠的一边的夹角为，将线段的长度表示为的函数；

（2）若从南面漂来一根长为7m的笔直的竹竿（粗细不计），竹竿始终浮于水平面内，且不发生形变，问：这根竹竿能否从拐角处一直漂向东西向的水渠（不会卡住）？请说明理由．

【题目】在平面直角坐标系xOy中，曲线C1的参数方程为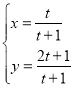（t为参数），曲线C2的参数方程为（α为参数），以坐标原点为极点.x轴正半轴为极轴建立极坐标系.

（Ⅰ）求曲线C1的普通方程和曲线C2的极坐标方程；

（Ⅱ）射线与曲线C2交于O，P两点，射线与曲线C1交于点Q，若△OPQ的面积为1，求|OP|的值.

【题目】已知函数.

（Ⅰ）若函数有两个零点，求a的取值范围；

（Ⅱ）恒成立，求a的取值范围.

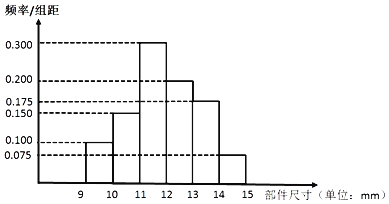
根据行业质量标准规定，该核心部件尺寸x满足：|x﹣12|≤1为一级品，1＜|x﹣12|≤2为二级品，|x﹣12|＞2为三级品.

（Ⅰ）现根据频率分布直方图中的分组，用分层抽样的方法先从这400件样本中抽取40件产品，再从所抽取的40件产品中，抽取2件尺寸x∈[12，15]的产品，记ξ为这2件产品中尺寸x∈[14，15]的产品个数，求ξ的分布列和数学期望；

（Ⅱ）将甲设备生产的产品成箱包装出售时，需要进行检验.已知每箱有100件产品，每件产品的检验费用为50元.检验规定：若检验出三级品需更换为一级或二级品；若不检验，让三级品进入买家，厂家需向买家每件支付200元补偿.现从一箱产品中随机抽检了10件，结果发现有1件三级品.若将甲设备的样本频率作为总体的慨率，以厂家支付费用作为决策依据，问是否对该箱中剩余产品进行一一检验？请说明理由；

（Ⅲ）为加大升级力度，厂家需增购设备.已知这种产品的利润如下：一级品的利润为500元/件；二级品的利润为400元/件；三级品的利润为200元/件.乙种设备产品中一、二、三级品的概率分别是，，.若将甲设备的样本频率作为总体的概率，以厂家的利润作为决策依据.应选购哪种设备？请说明理由.

【题目】已知F1，F2是椭圆C：（a＞b＞0）的左、右焦点，过椭圆的上顶点的直线x+y=1被椭圆截得的弦的中点坐标为.

（Ⅰ）求椭圆C的方程；

（Ⅱ）过F1的直线l交椭圆于A，B两点，当△ABF2面积最大时，求直线l的方程.

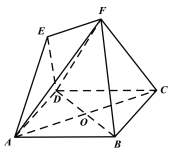
（Ⅰ）求证：BD⊥平面ACF；

（Ⅱ）求平面DEF与平面ABCD所成角的正弦值.

参考数据：若Z～N（μ，σ2），则P（μ﹣σ＜Z≤μ+σ）=0.6826，P（μ﹣2σ＜Z≤μ+2σ）=0.9544，P（μ﹣3σ＜Z≤μ+3σ）=0.9974

【题目】三棱锥中，，△为等边三角形，二面角的余弦值为，当三棱锥的体积最大时，其外接球的表面积为.则三棱锥体积的最大值为（ ）

A.B.C.D.