【题目】正方体的棱长为1，分别为的中点．则（ ）

A.直线与直线垂直B.直线与平面平行

C.平面截正方体所得的截面面积为D.点和点到平面的距离相等

A.财政预算内收入、城乡居民储蓄年末余额均呈增长趋势

B.财政预算内收入、城乡居民储蓄年末余额的逐年增长速度相同

C.财政预算内收入年平均增长量高于城乡居民储蓄年末余额年平均增长量

D.城乡居民储蓄年末余额与财政预算内收入的差额逐年增大

【题目】对于函数，若在定义域内存在实数，满足，则称为“类函数”.

（1）已知函数，试判断是否为“类函数”？并说明理由；

（2）设是定义域上的“类函数”，求实数的取值范围；

（3）若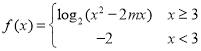为其定义域上的“类函数”，求实数取值范围.

【题目】设，函数.

（1）若，求函数在区间上的最大值；

（2）若，写出函数的单调区间（写出必要的过程，不必证明）；

（3）若存在，使得关于的方程有三个不相等的实数解，求实数的取值范围.

【题目】已知（，），，且函数图像上的任意两条对称轴之间距离的最小值是.

（1）求的值和的单调增区间；

（2）将函数的图像向右平移个单位后，得到函数的图像，求函数在上的最值，并求取得最值时的的值.

【题目】已知函数有两个不同零点、（），设函数的定义域为，且的最大值记为，最小值记为.

（1）求（用表示）；

（2）当时，试问以、、为长度的线段能否组成一个三角形，如果不一定，进一步求出的取值范围，使它们能组成一个三角形；

（3）求.

【题目】已知二次函数的定义域恰是不等式的解集，其值域为，函数的定义域为，值域为.

（1）求定义域和值域；

（2）试用单调性的定义法解决问题：若存在实数，使得函数在上单调递减，上单调递增，求实数的取值范围并用表示；

（3）是否存在实数，使成立？若存在，求实数的取值范围，若不存在，说明理由.

【题目】台风“山竹”导致海南省局部地方海啸，使当地的自来水受到了污染，某部门对水质监测后，决定往水中投放一种药剂来净化水质，已知每投放质量为的药剂后，经过天该药剂在水中释放的浓度（毫克/升）满足，其中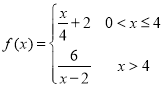，当药剂在水中释放的浓度不低于4（毫克/升）时称为有效净化，当药剂在水中释放的浓度不低于4（毫克/升）且不高于10（毫克/升）时称为最佳净化.

（1）如果投放的药剂质量为，试问自来水达到有效净化一共可持续几天？

（2）如果投放的药剂质量为，为了使在7天（从投放药剂算起包括第7天）之内的自来水达到最佳净化，试确定应该投放的药剂质量的值.

【题目】已知函数.

讨论的单调性.

若，求的取值范围.

【题目】若数列,满足,则称为数列的“偏差数列”.

（1）若为常数列,且为的“偏差数列”,试判断是否一定为等差数列,并说明理由;

（2）若无穷数列是各项均为正整数的等比数列,且,为数列的“偏差数列”,求的值;

（3）设,为数列的“偏差数列”,,且若对任意恒成立,求实数的最小值.