
科目: 来源: 题型:
【题目】某港口某天0时至24时的水深![]() (米)随时间
(米)随时间![]() (时)变化曲线近似满足如下函数模型
(时)变化曲线近似满足如下函数模型![]() (
(![]() ).若该港口在该天0时至24时内,有且只有3个时刻水深为3米,则该港口该天水最深的时刻不可能为( )
).若该港口在该天0时至24时内,有且只有3个时刻水深为3米,则该港口该天水最深的时刻不可能为( )
A.16时B.17时C.18时D.19时
查看答案和解析>>
科目: 来源: 题型:
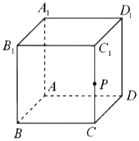
【题目】已知正方体![]() ,点
,点![]() 是棱
是棱![]() 的中点,设直线
的中点,设直线![]() 为
为![]() ,直线
,直线![]() 为
为![]() .对于下列两个命题:①过点
.对于下列两个命题:①过点![]() 有且只有一条直线
有且只有一条直线![]() 与
与![]() 、
、![]() 都相交;②过点
都相交;②过点![]() 有且只有一条直线
有且只有一条直线![]() 与
与![]() 、
、![]() 都成
都成![]() 角.以下判断正确的是( )
角.以下判断正确的是( )
A.①为真命题,②为真命题B.①为真命题,②为假命题
C.①为假命题,②为真命题D.①为假命题,②为假命题
查看答案和解析>>
科目: 来源: 题型:
【题目】近年来,人们的支付方式发生了巨大转变,使用移动支付购买商品已成为一部分人的消费习惯.某企业为了解该企业员工![]() 、
、![]() 两种移动支付方式的使用情况,从全体员工中随机抽取了100人,统计了他们在某个月的消费支出情况.发现样本中
两种移动支付方式的使用情况,从全体员工中随机抽取了100人,统计了他们在某个月的消费支出情况.发现样本中![]() ,
,![]() 两种支付方式都没有使用过的有5人;使用了
两种支付方式都没有使用过的有5人;使用了![]() 、
、![]() 两种方式支付的员工,支付金额和相应人数分布如下:
两种方式支付的员工,支付金额和相应人数分布如下:
支付金额(元) 支付方式 |
|
| 大于2000 |
使用 | 18人 | 29人 | 23人 |
使用 | 10人 | 24人 | 21人 |
依据以上数据估算:若从该公司随机抽取1名员工,则该员工在该月![]() 、
、![]() 两种支付方式都使用过的概率为______.
两种支付方式都使用过的概率为______.
查看答案和解析>>
科目: 来源: 题型:
【题目】现定义:设![]() 是非零实常数,若对于任意的
是非零实常数,若对于任意的![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 为“关于的
为“关于的![]() 偶型函数”
偶型函数”
(1)请以三角函数为例,写出一个“关于2的偶型函数”的解析式,并给予证明
(2)设定义域为的“关于的![]() 偶型函数”在区间
偶型函数”在区间![]() 上单调递增,求证在区间
上单调递增,求证在区间![]() 上单调递减
上单调递减
(3)设定义域为![]() 的“关于
的“关于![]() 的偶型函数”
的偶型函数”![]() 是奇函数,若
是奇函数,若![]() ,请猜测
,请猜测![]() 的值,并用数学归纳法证明你的结论
的值,并用数学归纳法证明你的结论
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线Γ的准线方程为![]() .焦点为
.焦点为![]() .
.
(1)求证:抛物线Γ上任意一点![]() 的坐标
的坐标![]() 都满足方程:
都满足方程:![]()
(2)请求出抛物线Γ的对称性和范围,并运用以上方程证明你的结论;
(3)设垂直于![]() 轴的直线与抛物线交于
轴的直线与抛物线交于![]() 两点,求线段
两点,求线段![]() 的中点
的中点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】请解答以下问题,要求解决两个问题的方法不同.
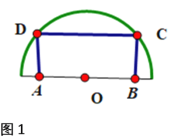
(1)如图1,要在一个半径为1米的半圆形铁板中截取一块面积最大的矩形![]() ,如何截取?并求出这个最大矩形的面积.
,如何截取?并求出这个最大矩形的面积.
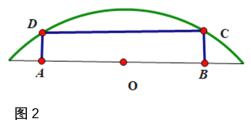
(2)如图2,要在一个长半轴为2米,短半轴为1米的半个椭圆铁板中截取一块面积最大的矩形![]() ,如何截取?并求出这个最大矩形的面积.
,如何截取?并求出这个最大矩形的面积.
查看答案和解析>>
科目: 来源: 题型:
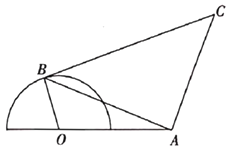
【题目】某生态农庄有一块如图所示的空地,其中半圆O的直径为300米,A为直径延长线上的点,![]() 米,B为半圆上任意一点,以AB为一边作等腰直角
米,B为半圆上任意一点,以AB为一边作等腰直角![]() ,其中BC为斜边.
,其中BC为斜边.
![]() 若
若![]() ;,求四边形OACB的面积;
;,求四边形OACB的面积;
![]() 现决定对四边形OACB区域地块进行开发,将
现决定对四边形OACB区域地块进行开发,将![]() 区域开发成垂钓中心,预计每平方米获利10元,将
区域开发成垂钓中心,预计每平方米获利10元,将![]() 区域开发成亲子采摘中心,预计每平方米获利20元,则当
区域开发成亲子采摘中心,预计每平方米获利20元,则当![]() 为多大时,垂钓中心和亲子采摘中心获利之和最大?
为多大时,垂钓中心和亲子采摘中心获利之和最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为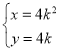 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)已知点![]() ,且直线
,且直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值
的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com