
科目: 来源: 题型:
【题目】某学习小组在生物研究性学习中,对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究,于是小组成员在3月份的31天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下资料:
日期 | 3月2日 | 3月8日 | 3月15日 | 3月22日 | 3月28日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 14 |
(1)在这个学习小组中负责统计数据的那位同学为了减少计算量,他从这5天中去掉了3月2日与3月28日的两组数据,请根据这5天中的另三天的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若由线性回归方程得到的估计数据与所去掉的试验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
(参考公式: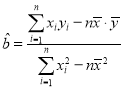 ,
,![]() )(参考数据:
)(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】公元263年左右,我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率![]() ,他从单位圆内接正六边形算起,令边数一倍一倍地增加,即12,24,48,…,192,…,逐个算出正六边形,正十二边形,正二十四边形,…,正一百九十二边形,…的面积,这些数值逐步地逼近圆面积,刘徽算到了正一百九十二边形,这时候
,他从单位圆内接正六边形算起,令边数一倍一倍地增加,即12,24,48,…,192,…,逐个算出正六边形,正十二边形,正二十四边形,…,正一百九十二边形,…的面积,这些数值逐步地逼近圆面积,刘徽算到了正一百九十二边形,这时候![]() 的近似值是3.141024,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽这种想法的可贵之处在于用已知的、可求的来逼近未知的、要求的,用有限来逼近无穷,这种思想极其重要,对后世产生了巨大影响.按照上面“割圆术”,用正二十四边形来估算圆周率,则
的近似值是3.141024,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽这种想法的可贵之处在于用已知的、可求的来逼近未知的、要求的,用有限来逼近无穷,这种思想极其重要,对后世产生了巨大影响.按照上面“割圆术”,用正二十四边形来估算圆周率,则![]() 的近似值是( )(精确到
的近似值是( )(精确到![]() ).(参考数据
).(参考数据![]() )
)
A.3.14B.3.11C.3.10D.3.05
查看答案和解析>>
科目: 来源: 题型:
【题目】对于定义域为R的函数y=f(x),部分x与y的对应关系如表:
x | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 0 | 2 | 3 | 2 | 0 | ﹣1 | 0 | 2 |
(1)求f{f[f(0)]};
(2)数列{xn}满足x1=2,且对任意n∈N*,点(xn,xn+1)都在函数y=f(x)的图象上,求x1+x2+…+x4n;
(3)若y=f(x)=Asin(ωx+φ)+b,其中A>0,0<ω<π,0<φ<π,0<b<3,求此函数的解析式,并求f(1)+f(2)+…+f(3n)(n∈N*).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C:![]() =1(a>b>0),定义椭圆C上的点M(x0,y0)的“伴随点”为
=1(a>b>0),定义椭圆C上的点M(x0,y0)的“伴随点”为![]() .
.
(1)求椭圆C上的点M的“伴随点”N的轨迹方程;
(2)如果椭圆C上的点(1,![]() )的“伴随点”为(
)的“伴随点”为(![]() ,
,![]() ),对于椭圆C上的任意点M及它的“伴随点”N,求
),对于椭圆C上的任意点M及它的“伴随点”N,求![]() 的取值范围;
的取值范围;
(3)当a=2,b=![]() 时,直线l交椭圆C于A,B两点,若点A,B的“伴随点”分别是P,Q,且以PQ为直径的圆经过坐标原点O,求△OAB的面积.
时,直线l交椭圆C于A,B两点,若点A,B的“伴随点”分别是P,Q,且以PQ为直径的圆经过坐标原点O,求△OAB的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图ABC﹣A1B1C1是直三棱柱,底面△ABC是等腰直角三角形,且AB=AC=4,直三棱柱的高等于4,线段B1C1的中点为D,线段BC的中点为E,线段CC1的中点为F.
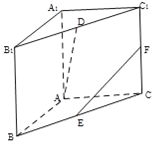
(1)求异面直线AD、EF所成角的大小;
(2)求三棱锥D﹣AEF的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知平面直角坐标系![]() ,以
,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),点
为参数),点![]() 时曲线
时曲线![]() 上两点,点
上两点,点![]() 的极坐标分别为
的极坐标分别为![]() ,
,![]() .
.
(1)写出曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() 与抛物线
与抛物线![]() 有一条斜率为1的公共切线
有一条斜率为1的公共切线![]() .
.
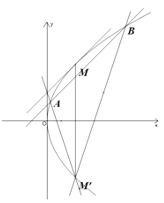
(1)求![]() .
.
(2)设![]() 与抛物线切于点
与抛物线切于点![]() ,作点
,作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,在区域
,在区域![]() 内过
内过![]() 作两条关于直线
作两条关于直线![]() 对称的抛物线的弦
对称的抛物线的弦![]() ,
,![]() .连接
.连接![]() .
.
①求证:![]() ;
;
②设![]() 面积为
面积为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市对各老旧小区环境整治效果进行满意度测评,共有10000人参加这次测评(满分100分,得分全为整数).为了解本次测评分数情况,从中随机抽取了部分人的测评分数进行统计,整理见下表:
组别 | 分组 | 频数 | 频率 |
1 |
| 3 | 0.06 |
2 |
| 15 | 0.3 |
3 |
| 21 |
|
4 |
| 3 | 0.12 |
5 |
|
| 0.1 |
合计 |
| 1.00 | |
(1)求出表中![]() ,
,![]() ,
,![]() 的值;
的值;
(2)若分数在80(含80分)以上表示对该项目“非常满意”,其中分数在90(含90分)以上表示“十分满意”,现从被抽取的“非常满意“人群中随机抽取2人,求至少有一人分数是“十分满意”的概率;
(3)请你根据样本数据估计全市的平均测评分数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com