
科目: 来源: 题型:
【题目】如图,某公园有三条观光大道![]() 围成直角三角形,其中直角边
围成直角三角形,其中直角边![]() ,斜边
,斜边![]() .现有甲、乙、丙三位小朋友分别在
.现有甲、乙、丙三位小朋友分别在![]() 大道上嬉戏,所在位置分别记为点
大道上嬉戏,所在位置分别记为点![]() .
.
(1)若甲乙都以每分钟![]() 的速度从点
的速度从点![]() 出发在各自的大道上奔走,到大道的另一端
出发在各自的大道上奔走,到大道的另一端
时即停,乙比甲迟2分钟出发,当乙出发1分钟后,求此时甲乙两人之间的距离;
(2)设![]() ,乙丙之间的距离是甲乙之间距离的2倍,且
,乙丙之间的距离是甲乙之间距离的2倍,且![]() ,请将甲
,请将甲
乙之间的距离![]() 表示为θ的函数,并求甲乙之间的最小距离.
表示为θ的函数,并求甲乙之间的最小距离.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某公园内有一块矩形绿地区域ABCD,已知AB=100米,BC=80米,以AD,BC为直径的两个半圆内种植花草,其它区域种值苗木. 现决定在绿地区域内修建由直路BN,MN和弧形路MD三部分组成的观赏道路,其中直路MN与绿地区域边界AB平行,直路为水泥路面,其工程造价为每米2a元,弧形路为鹅卵石路面,其工程造价为每米3a元,修建的总造价为W元. 设![]() .
.
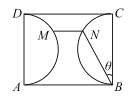
(1)求W关于![]() 的函数关系式;
的函数关系式;
(2)如何修建道路,可使修建的总造价最少?并求最少总造价.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某景区内有一半圆形花圃,其直径AB为6,O是圆心,且OC⊥AB.在OC上有一座观赏亭Q,其中∠AQC=![]() ,.计划在
,.计划在![]() 上再建一座观赏亭P,记∠POB=θ
上再建一座观赏亭P,记∠POB=θ![]() .
.
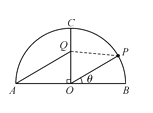
(1)当θ=![]() 时,求∠OPQ的大小;
时,求∠OPQ的大小;
(2)当∠OPQ越大时,游客在观赏亭P处的观赏效果越佳,求游客在观赏亭P处的观赏效果最佳时,角θ的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1所示为一种魔豆吊灯,图2为该吊灯的框架结构图,由正六棱锥![]() 和
和![]() 构成,两个棱锥的侧棱长均相等,且棱锥底面外接圆的直径为
构成,两个棱锥的侧棱长均相等,且棱锥底面外接圆的直径为![]() ,底面中心为
,底面中心为![]() ,通过连接线及吸盘固定在天花板上,使棱锥的底面呈水平状态,下顶点
,通过连接线及吸盘固定在天花板上,使棱锥的底面呈水平状态,下顶点![]() 与天花板的距离为
与天花板的距离为![]() ,所有的连接线都用特殊的金属条制成,设金属条的总长为y.
,所有的连接线都用特殊的金属条制成,设金属条的总长为y.
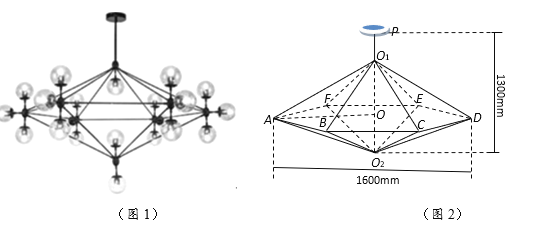
(1)设∠O1AO =![]() (rad),将y表示成θ的函数关系式,并写出θ的范围;
(rad),将y表示成θ的函数关系式,并写出θ的范围;![]()
(2)请你设计θ,当角θ正弦值的大小是多少时,金属条总长y最小.
查看答案和解析>>
科目: 来源: 题型:
【题目】某景区修建一栋复古建筑,其窗户设计如图所示.圆![]() 的圆心与矩形
的圆心与矩形![]() 对角线的交点重合,且圆与矩形上下两边相切(
对角线的交点重合,且圆与矩形上下两边相切(![]() 为上切点),与左右两边相交(
为上切点),与左右两边相交(![]() ,
,![]() 为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1
为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1![]() ,且
,且![]() ,设
,设![]() ,透光区域的面积为
,透光区域的面积为![]() .
.
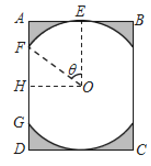
(1)求![]() 关于
关于![]() 的函数关系式,并求出定义域;
的函数关系式,并求出定义域;
(2)根据设计要求,透光区域与矩形窗面的面积比值越大越好.当该比值最大时,求边![]() 的长度.
的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】某农场有一块农田,如图所示,它的边界由圆O的一段圆弧![]() (P为此圆弧的中点)和线段MN构成.已知圆O的半径为40米,点P到MN的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD,大棚Ⅱ内的地块形状为
(P为此圆弧的中点)和线段MN构成.已知圆O的半径为40米,点P到MN的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD,大棚Ⅱ内的地块形状为![]() ,要求
,要求![]() 均在线段
均在线段![]() 上,
上,![]() 均在圆弧上.设OC与MN所成的角为
均在圆弧上.设OC与MN所成的角为![]() .
.
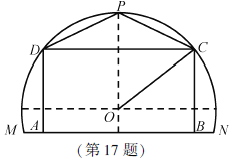
(1)用![]() 分别表示矩形
分别表示矩形![]() 和
和![]() 的面积,并确定
的面积,并确定![]() 的取值范围;
的取值范围;
(2)若大棚Ⅰ内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为![]() .求当
.求当![]() 为何值时,能使甲、乙两种蔬菜的年总产值最大.
为何值时,能使甲、乙两种蔬菜的年总产值最大.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一个湖的边界是圆心为O的圆,湖的一侧有一条直线型公路l,湖上有桥AB(AB是圆O的直径).规划在公路l上选两个点P、Q,并修建两段直线型道路PB、QA.规划要求:线段PB、QA上的所有点到点O的距离均不小于圆O的半径.已知点A、B到直线l的距离分别为AC和BD(C、D为垂足),测得AB=10,AC=6,BD=12(单位:百米).
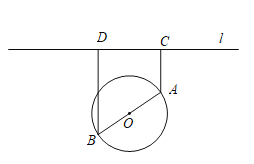
(1)若道路PB与桥AB垂直,求道路PB的长;
(2)在规划要求下,P和Q中能否有一个点选在D处?并说明理由;
(3)对规划要求下,若道路PB和QA的长度均为d(单位:百米).求当d最小时,P、Q两点间的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】某无缝钢管厂只生产甲、乙两种不同规格的钢管,钢管有内外两个口径,甲种钢管内外两口径的标准长度分别为![]() 和
和![]() ,乙种钢管内外两个口径的标准长度分别为
,乙种钢管内外两个口径的标准长度分别为![]() 和
和![]() .根据长期的生产结果表明,两种规格钢管每根的长度
.根据长期的生产结果表明,两种规格钢管每根的长度![]() 都服从正态分布
都服从正态分布![]() ,长度在
,长度在![]() 之外的钢管为废品,要回炉熔化,不准流入市场,其他长度的钢管为正品.
之外的钢管为废品,要回炉熔化,不准流入市场,其他长度的钢管为正品.
(1)在该钢管厂生产的钢管中随机抽取10根进行检测,求至少有1根为废品的概率;
(2)监管部门规定每种规格钢管的“口径误差”的计算方式为:若钢管的内外两个口径实际长分别为![]() ,标准长分别为
,标准长分别为![]() ,则“口径误差”为
,则“口径误差”为![]() ,按行业生产标准,其中“一级品”“二级品”“合格品”的“口径误差”的范围分别是
,按行业生产标准,其中“一级品”“二级品”“合格品”的“口径误差”的范围分别是![]() (正品钢管中没有“口径误差”大于
(正品钢管中没有“口径误差”大于![]() 的钢管),现分别从甲、乙两种产品的正品中各随机抽取100根,分别进行“口径误差”的检测,统计后,绘制其频率分布直方图如图所示:
的钢管),现分别从甲、乙两种产品的正品中各随机抽取100根,分别进行“口径误差”的检测,统计后,绘制其频率分布直方图如图所示:
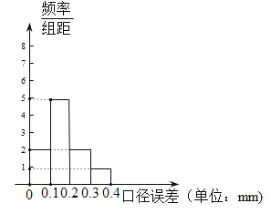

甲种钢管 乙种钢管
已知经销商经销甲种钢管,其中“一级品”的利润率为0.3,“二级品”的利润率为0.18,“合格品”的利润率为0.1;经销乙种钢管,其中“一级品”的利润率为0.25,“二级品”的利润率为0.15,“合格品”的利润率为0.08,若视频率为概率.
(ⅰ)若经销商对甲、乙两种钢管各进了100万元的货,![]() 和
和![]() 分别表示经销甲、乙两种钢管所获得的利润,求
分别表示经销甲、乙两种钢管所获得的利润,求![]() 和
和![]() 的数学期望和方差,并由此分析经销商经销两种钢管的利弊;
的数学期望和方差,并由此分析经销商经销两种钢管的利弊;
(ⅱ)若经销商计划对甲、乙两种钢管总共进100万元的货,则分别在甲、乙两种钢管上进货多少万元时,可使得所获利润的方差和最小?
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com