A.0B.1C.2D.3

【题目】已知函数.

（1）讨论函数的极值点的个数；

（2）当函数有两个极值点，时，求证：.

【题目】已知点C是平面直角坐标系中的一个动点，过点C且与y轴垂直的直线与直线交于点M，若向量与向量垂直，其中O为坐标原点.

（1）求点C的轨迹方程E；

（2）过曲线E的焦点作互相垂直的两条直线分别交曲线E于A，B，P，Q四点，求四边形APBQ的面积的最小值.

（1）若y与x具有线性相关关系，请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程，并预测第六天销售该洗发液的瓶数（按四舍五入取到整数）；

（2）超市打算第六天加大活动力度，购买洗发液可参加抽奖，中奖者可领取奖金20元，中奖概率为，已知甲、乙两名顾客抽奖中奖与否相互独立，求甲、乙所获得奖金之和X的分布列及数学期望.

参考公式：，.

【题目】如图，在四棱锥中，平面平面ABCD，底面ABCD是直角梯形，，，，O是AD的中点.

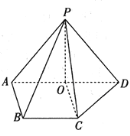
（1）在线段PA上找一点E，使得平面PCD，并证明；

（2）在（1）的条件下，若，求平面OBE与平面POC所成的锐二面角的余弦值.

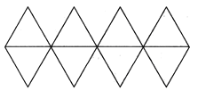
【题目】蹴鞠起源于春秋战国，是现代足球的前身.到了唐代，制作的蹴鞠已接近于现代足球，做法是：用八片鞣制好的尖皮缝制成“圆形”的球壳，在球壳内放一个动物膀胱，“嘘气闭而吹之”，成为充气的球.如图所示，将八个全等的正三角形缝制成一个空间几何体，在几何体内放一个气球，往气球内充气使几何体膨胀，当几何体膨胀成球体（顶点位置不变）且恰好是原几何体外接球时，测得球的体积是，则正三角形的边长为（ ）

A.B.C.D.

【题目】已知函数.

（1）讨论的单调性；

（2）若有两个极值点，当时，求的最大值.

【题目】已知在四棱锥中，，，是的中点，是等边三角形，平面平面.

（1）求证：平面；

（2）求二面角的余弦值.

【题目】在①；②，这两个条件中任选一个，补充在下面问题中，然后解答补充完整的题目.

在中，内角的对边分别为，设的面积为，已知 .

（1）求的值；

（2）若，求的值.

注：如果选择多个条件分别解答，按第一个解答计分.

【题目】某销售公司在当地、两家超市各有一个销售点，每日从同一家食品厂一次性购进一种食品，每件200元，统一零售价每件300元，两家超市之间调配食品不计费用，若进货不足食品厂以每件250元补货，若销售有剩余食品厂以每件150回收.现需决策每日购进食品数量，为此搜集并整理了、两家超市往年同期各50天的该食品销售记录，得到如下数据：

以这些数据的频数代替两家超市的食品销售件数的概率，记表示这两家超市每日共销售食品件数，表示销售公司每日共需购进食品的件数.

（1）求的分布列；

（2）以销售食品利润的期望为决策依据，在与之中选其一，应选哪个？