游戏准备：

选取甲、乙两位小朋友面朝同一方向并排坐下进行游戏．教师站在两位小朋友面前出示游戏卡片．游戏卡片为两张白色纸板，一张纸板正反两面都打印有相同的”左“字，另一张纸板正反两面打印有相同的“右”字．

游戏进行：

一轮游戏（一轮游戏包含多次游戏直至决出胜者）开始后，教师站在参加游戏的甲、乙两位小朋友面前出示游戏卡片并大声报出出示的卡片上的“左”或者“右”字．两位小朋友如果听到“左”的指令，或者看到教师出示写有“左”字的卡片就应当将左手放至右肩上并大声喊出“停!”．小朋友如果听到“右”的指令，或者看到教师出示写有“右”字的卡片就应当将右手放至左肩上并大声喊出“停!”．最先完成指令动作的小朋友喊出“停!”时，两位小朋友都应当停止动作，教师根据两位小朋友的动作完成情况进行评分，至此游戏完成一次．

游戏评价：

为了方便描述问题，约定：对于每次游戏，若甲小朋友正确完成了指令动作且乙小朋友未完成则甲得1分，乙得﹣1分；若乙小朋友正确完成了指令动作且甲小朋友未完成则甲得﹣1分，乙得1分；若甲，乙两位小朋友都正确完成或都未正确完成指令动作，则两位小朋友均得0分．当两位小朋友中的一位比另外一位小朋友的分数多8分时，就停止本轮游戏，并判定得分高的小朋友获胜．现假设“甲小朋友能正确完成一次游戏中的指令动作的概率为α，乙小朋友能正确完成一次游戏中的指令动作的概率为β”，一次游戏中甲小朋友的得分记为X．

（1）求X的分布列；

（2）若甲小朋友、乙小朋友在一轮游戏开始时都赋予4分，pi（i＝0，1，…，8）表示“甲小朋友的当前累计得分为i时，本轮游戏甲小朋友最终获胜”的概率，则P0＝0，p8＝1，pi＝api﹣1+bpi+cpi+1（i＝1，2，…，7），其中a＝P（X＝﹣1），b＝P（X＝0），c＝P（X＝1）．假设α＝0.5，β＝0.8．

①证明：{pi+1﹣pi}（i＝0，1，2，…，7）为等比数列；

②求p4，并根据p4的值说明这种游戏方案是否能够充分验证“甲小朋友能正确完成一次游戏中的指令动作的概率为0.5，乙小朋友能正确完成一次游戏中的指令动作的率为0.8”的假设．

【题目】在平面直角坐标系xOy中，已知抛物线C：的焦点为F，过F的直线交抛物线C于A，B两点．

（1）求线段AF的中点M的轨迹方程；

（2）已知△AOB的面积是△BOF面积的3倍，求直线的方程．

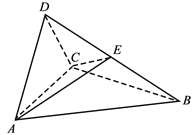
（1）证明：平面ACD⊥平面ABC；

（2）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D–AE–C的余弦值.

【题目】A4纸是生活中最常用的纸规格．A系列的纸张规格特色在于：①A0、A1、A2…、A5，所有尺寸的纸张长宽比都相同．②在A系列纸中，前一个序号的纸张以两条长边中点连线为折线对折裁剪分开后，可以得到两张后面序号大小的纸，比如1张A0纸对裁后可以得到2张A1纸，1张A1纸对裁可以得到2张A2纸，依此类推．这是因为A系列纸张的长宽比为：1这一特殊比例，所以具备这种特性．已知A0纸规格为84.1厘米×118.9厘米.118.9÷84.1≈1.41≈，那么A4纸的长度为（　　）

A.厘米B.厘米C.厘米D.厘米

【题目】已知直线的斜率为，纵截距为.

（1）求点（2，4）关于直线的对称点坐标；

（2）求与直线平行且距离为的直线方程.

【题目】已知函数在点处的切线方程为.

（1）若函数存在单调递减区间，求实数的取值范围；

（2）设，对于，的值域为，若，求实数的取值范围.

【题目】已知椭圆的左、右焦点为，左右两顶点，点为椭圆上任意一点，满足直线的斜率之积为，且的最大值为4.

（1）求椭圆的标准方程；

（2）已知直线与轴的交点为，过点的直线与椭圆相交与两点，连接点并延长，交轨迹于一点.求证：.

【题目】在如图（1）梯形中，，过作于，，沿翻折后得图（2），使得，又点满足，连接，且.

（1）证明：平面；

（2）求平面与平面所成的二面角的余弦值.

（1）此栏目编导对本期的40位大众评委的年龄和对京剧知识的了解进行调查，根据调查得到的数据如下：

试问：在犯错误的概率不超过多少的前提下，可以认为年龄的大小与对京剧知识的了解有关系？

（2）若在一轮中演唱中，每猜出一位亮相一位，且规定猜出2位“梅派”传人”或猜出5人后就终止，记本轮竞猜一共竞猜次，求随机变量的分布列与期望.

参考数据：

参考公式：

【题目】如图，已知六个直角边均为1和的直角三角形围成的两个正六边形，则该图形绕着旋转一周得到的几何体的体积为（ ）

A.B.C.D.