
����Ŀ��Ϊ����������С���ѳ����Կ����������ֺ����֣������Ҽ磬����Ϸ�����ϸ��Ϸ��ͱ��������ͬʱ�ܴر����Լ����뷨��������ͬ����Ϸ�Ŀ��֣�ijλ��ʦ�����һ����Ϊ���������ң�����Ϸ���������£�
��Ϸ����
ѡȡ�ס�����λС�����泯ͬһ���������½�����Ϸ����ʦվ����λС������ǰ��ʾ��Ϸ��Ƭ����Ϸ��ƬΪ���Ű�ɫֽ�壬һ��ֽ���������涼��ӡ����ͬ�ġ����֣���һ��ֽ�����������ӡ����ͬ�ġ��ҡ��֣�
��Ϸ���У�
һ����Ϸ��һ����Ϸ���������Ϸֱ������ʤ�ߣ���ʼ��ʦվ�ڲμ���Ϸ�ļס�����λС������ǰ��ʾ��Ϸ��Ƭ������������ʾ�Ŀ�Ƭ�ϵġ����ߡ��ҡ��֣���λС���������������ָ����߿�����ʦ��ʾд�С����ֵĿ�Ƭ��Ӧ�������ַ����Ҽ��ϲ�����������ͣ!����С��������������ҡ���ָ����߿�����ʦ��ʾд�С��ҡ��ֵĿ�Ƭ��Ӧ�������ַ�������ϲ�����������ͣ!�����������ָ�����С���Ѻ�����ͣ!��ʱ����λС���Ѷ�Ӧ��ֹͣ��������ʦ������λС���ѵĶ����������������֣�������Ϸ���һ�Σ�
��Ϸ���ۣ�
Ϊ�˷����������⣬Լ��������ÿ����Ϸ������С������ȷ�����ָ�������С����δ������1�֣��ҵé�1�֣�����С������ȷ�����ָ����Ҽ�С����δ�����é�1�֣��ҵ�1�֣����ף�����λС���Ѷ���ȷ��ɻ�δ��ȷ���ָ���������λС���Ѿ���0�֣�����λС�����е�һλ������һλС���ѵķ�����8��ʱ����ֹͣ������Ϸ�����ж��÷ָߵ�С���ѻ�ʤ���ּ��衰��С��������ȷ���һ����Ϸ�е�ָ����ĸ���Ϊ������С��������ȷ���һ����Ϸ�е�ָ����ĸ���Ϊ������һ����Ϸ�м�С���ѵĵ÷ּ�ΪX��
��1����X�ķֲ��У�
��2������С���ѡ���С������һ����Ϸ��ʼʱ������4�֣�pi��i��0��1������8����ʾ����С���ѵĵ�ǰ�ۼƵ÷�Ϊiʱ��������Ϸ��С�������ջ�ʤ���ĸ��ʣ���P0��0��p8��1��pi��api��1+bpi+cpi+1��i��1��2������7��������a��P��X����1����b��P��X��0����c��P��X��1������������0.5������0.8��
��֤����{pi+1��pi}��i��0��1��2������7��Ϊ�ȱ����У�
����p4��������p4��ֵ˵��������Ϸ�����Ƿ��ܹ������֤����С��������ȷ���һ����Ϸ�е�ָ����ĸ���Ϊ0.5����С��������ȷ���һ����Ϸ�е�ָ�������Ϊ0.8���ļ��裮
���𰸡���1���ֲ��м�������2����֤������������p4��![]() �����ܹ�
�����ܹ�
��������
��1�������![]() �����п���ȡֵ������
�����п���ȡֵ������![]() ��ʾ��
��ʾ��![]() ȡ����ֵʱ�ĸ��ʣ����ɵ�X�ķֲ���.
ȡ����ֵʱ�ĸ��ʣ����ɵ�X�ķֲ���.
��2�����ɣ�1����![]() ��ֵ�������õȱ����еĶ��壬֤������{pi+1��pi}��i��0��1��2������7��Ϊ�ȱ����У������âٵĽ��ۣ���
��ֵ�������õȱ����еĶ��壬֤������{pi+1��pi}��i��0��1��2������7��Ϊ�ȱ����У������âٵĽ��ۣ���![]() ��
��![]() ��ʾ���ٸ���
��ʾ���ٸ���![]() �������
�������![]() ���Ӷ���
���Ӷ���![]() ��ֵ��������֤����.
��ֵ��������֤����.
��1��![]() �����п���ȡֵΪ
�����п���ȡֵΪ![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
����X�ķֲ���Ϊ��
| | | |
| | | |
��2���� �ɣ�1����![]() ��
��![]() ��
��![]()
���![]() ����
����![]() ��
��
��![]() ��
��
����Ϊ![]() ��
��
����{pi+1��pi}��i��0��1��2������7��Ϊ����Ϊ![]() ������Ϊ
������Ϊ![]() �ȱ�����.
�ȱ�����.
�� �ɢٿɵ�![]()
![]()
![]() ��
��
����![]() ����
����![]() ��
��
����![]()
![]() ��
��
![]() ��ʾ���ռ�ʤ�ĸ��ʣ��ɼ��������Կ���������С��������ȷ���һ����Ϸ�е�ָ����ĸ���Ϊ0.5����С��������ȷ���һ����Ϸ�е�ָ�������Ϊ0.8�������ܻ�ʤ�ĸ���Ϊ
��ʾ���ռ�ʤ�ĸ��ʣ��ɼ��������Կ���������С��������ȷ���һ����Ϸ�е�ָ����ĸ���Ϊ0.5����С��������ȷ���һ����Ϸ�е�ָ�������Ϊ0.8�������ܻ�ʤ�ĸ���Ϊ![]() ����ʱ�ó�����Ľ��۵ĸ��ʷdz�С�����ܳ����֤��������ļ���.
����ʱ�ó�����Ľ��۵ĸ��ʷdz�С�����ܳ����֤��������ļ���.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() ������
������![]() ��
��![]() ��Ϊʵ����
��Ϊʵ����
��1����![]() ʱ�����ۺ���
ʱ�����ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
��2����![]() ʱ������ʽ
ʱ������ʽ![]() ��
��![]() �Ϻ��������ʵ��
�Ϻ��������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����![]() ����
����![]() ʱ��֤����
ʱ��֤����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������6̨���ͻ�������1�����У�1̨�����������1�ι��ϣ���ÿ̨�����Ƿ���ֹ�����������ģ����ֹ���ʱ��1�����˽���ά�ޣ�ÿ̨�������ֹ��ϵĸ���Ϊ![]() .��֪1������ÿ��ֻ��ά��2̨����������������2̨����ͬʱ���ֹ��ϣ�����ֻ��1��ά���ˣ���ù���ֻ����̨ά�ޣ��Թ�������������û���κ�Ӱ�죩��ÿ̨���������ֹ��ϻ���ֹ���ʱ�ܼ�ʱ�õ�ά�ޣ�����ʹ�ó����10��Ԫ����������2��Ԫ.�ù���ÿ����֧����ÿ��ά����1��Ԫ�Ĺ���.
.��֪1������ÿ��ֻ��ά��2̨����������������2̨����ͬʱ���ֹ��ϣ�����ֻ��1��ά���ˣ���ù���ֻ����̨ά�ޣ��Թ�������������û���κ�Ӱ�죩��ÿ̨���������ֹ��ϻ���ֹ���ʱ�ܼ�ʱ�õ�ά�ޣ�����ʹ�ó����10��Ԫ����������2��Ԫ.�ù���ÿ����֧����ÿ��ά����1��Ԫ�Ĺ���.
��1����ÿ̨�����ڵ��²����ֹ��ϻ���ֹ���ʱ���й��˽���ά�ޣ����磺3̨���ͻ������ֹ��ϣ���������Ҫ2��ά���ˣ�����ƹ�������������.���ó�ֻ��1��ά���ˣ���ÿ�����������еĸ��ʣ�
��2����֪�ó�����2��ά����.
�������Ǹó�ÿ�»���Ϊ![]() ��Ԫ����
��Ԫ����![]() �ķֲ�������ѧ������
�ķֲ�������ѧ������
�������Թ���ÿ�»�������ѧ����Ϊ�������ݣ����ʸó��Ƿ�Ӧ����Ƹ1��ά���ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��1������![]() �У�
��![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ���ۺ��ͼ��2����ʹ��
���ۺ��ͼ��2����ʹ��![]() ���ֵ�
���ֵ�![]() ����
����![]() ������
������![]() ����
����![]() .
.

��1��֤����![]() ƽ��
ƽ��![]() ��
��
��2��������![]() ���������.
���������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �ڵ�
�ڵ�![]() �������߷���Ϊ
�������߷���Ϊ![]() .
.
��1��������![]() ���ڵ����ݼ����䣬��ʵ��
���ڵ����ݼ����䣬��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() ������
������![]() ��
��![]() ��ֵ��Ϊ
��ֵ��Ϊ![]() ����
����![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��ֱ��
��ֱ��![]() ��������
��������![]() ����
����![]() ��
��![]() ���㣬��
���㣬��![]() ��
��![]() ����Ϊ�е�ֱ���������
����Ϊ�е�ֱ���������![]() ������
������![]() ��
��![]() ����
����![]() ��
��![]() ���ڵ�
���ڵ�![]() .
.
��1����![]() ��
��
��2����![]() ��
��![]() ��ֱ�߽�������
��ֱ�߽�������![]() ��
��![]() ��
��![]() ���㣬֤����
���㣬֤����![]() �������ı���
�������ı���![]() �������Сֵ.
�������Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCDPN�У���PA����ABCD��AB=AP=2PN������ABCD�����Σ���BAD=![]() ��
��

��1����֤��PN��AB��
��2����NC��ƽ��BDN���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ı���ABCD��BDEF��Ϊ���Σ�![]() ����
����![]() ��
��
![]() ��֤��
��֤��![]() ƽ��BDEF��
ƽ��BDEF��
![]() ��ֱ��AD��ƽ��ABF���ɽǵ�����ֵ��
��ֱ��AD��ƽ��ABF���ɽǵ�����ֵ��
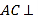
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ��ˮ���ľ����������ˮ��ÿ�յ�������![]() ����λ��ǧ�ˣ������ۼ۸�
����λ��ǧ�ˣ������ۼ۸�![]() ����λ��Ԫ/ǧ�ˣ������ϵʽ
����λ��Ԫ/ǧ�ˣ������ϵʽ![]() ������
������![]() ��
��![]() Ϊ����.��֪���ۼ۸�Ϊ6Ԫ/ǧ��ʱ��ÿ�տ��۳���ˮ��52ǧ��.
Ϊ����.��֪���ۼ۸�Ϊ6Ԫ/ǧ��ʱ��ÿ�տ��۳���ˮ��52ǧ��.
��1����![]() ��ֵ��
��ֵ��
��2������ˮ���ijɱ�Ϊ5Ԫ/ǧ�ˣ���ȷ�����ۼ۸�![]() ��ֵ��ʹ�̳�ÿ�����۸�ˮ������õ������������������.
��ֵ��ʹ�̳�ÿ�����۸�ˮ������õ������������������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com