
【题目】某商场销售一种水果的经验表明,该水果每日的销售量![]() (单位:千克)与销售价格
(单位:千克)与销售价格![]() (单位:元/千克)满足关系式
(单位:元/千克)满足关系式![]() ,其中
,其中![]() ,
,![]() 为常数.已知销售价格为6元/千克时,每日可售出该水果52千克.
为常数.已知销售价格为6元/千克时,每日可售出该水果52千克.
(1)求![]() 的值;
的值;
(2)若该水果的成本为5元/千克,试确定销售价格![]() 的值,使商场每日销售该水果所获得的利润最大,并求出最大利润.
的值,使商场每日销售该水果所获得的利润最大,并求出最大利润.
【答案】(1)![]() ;(2)
;(2)![]() ,66元.
,66元.
【解析】
(1)由销售价格为6元/千克时,每日可售出该水果52千克;建立方程,即可求出![]() 的值;
的值;
(2)商场每日销售该水果所获得的利润![]() 每日的销售量
每日的销售量![]() 销售该水果的单利润,可得日销售量的利润函数为关于
销售该水果的单利润,可得日销售量的利润函数为关于![]() 的三次多项式函数,再用求导数的方法讨论函数的单调性,得出函数的极大值点,从而得出最大值对应的
的三次多项式函数,再用求导数的方法讨论函数的单调性,得出函数的极大值点,从而得出最大值对应的![]() 值.
值.
(1)因为![]() 时,
时,![]() ,所以
,所以![]() ,
,![]() .
.
(2)由(1)可知,该水果每日的销售量为![]() ,
,
所以商场每日销售该水果所获得的利润为
![]() ,
,![]() ,
,
从而![]()
![]() ,
,
于是,当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
| 7 |
|
| + | 0 | - |
| 单调递增 | 极大值66 | 单调递减 |
由上表可得,![]() 时,函数
时,函数![]() 取得极大值,也是最大值.
取得极大值,也是最大值.
所以,当销售价格为7元/千克时,商场每日销售该水果所获得的利润最大,为66元.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了让幼儿园大班的小朋友尝试以客体区分左手和右手,左肩和右肩,在游戏中提高细致戏察和辨别能力,同时能大胆地表达自己的想法,体验与同伴游戏的快乐,某位教师设计了一个名为(肩手左右)的游戏,方案如下:
游戏准备:
选取甲、乙两位小朋友面朝同一方向并排坐下进行游戏.教师站在两位小朋友面前出示游戏卡片.游戏卡片为两张白色纸板,一张纸板正反两面都打印有相同的”左“字,另一张纸板正反两面打印有相同的“右”字.
游戏进行:
一轮游戏(一轮游戏包含多次游戏直至决出胜者)开始后,教师站在参加游戏的甲、乙两位小朋友面前出示游戏卡片并大声报出出示的卡片上的“左”或者“右”字.两位小朋友如果听到“左”的指令,或者看到教师出示写有“左”字的卡片就应当将左手放至右肩上并大声喊出“停!”.小朋友如果听到“右”的指令,或者看到教师出示写有“右”字的卡片就应当将右手放至左肩上并大声喊出“停!”.最先完成指令动作的小朋友喊出“停!”时,两位小朋友都应当停止动作,教师根据两位小朋友的动作完成情况进行评分,至此游戏完成一次.
游戏评价:
为了方便描述问题,约定:对于每次游戏,若甲小朋友正确完成了指令动作且乙小朋友未完成则甲得1分,乙得﹣1分;若乙小朋友正确完成了指令动作且甲小朋友未完成则甲得﹣1分,乙得1分;若甲,乙两位小朋友都正确完成或都未正确完成指令动作,则两位小朋友均得0分.当两位小朋友中的一位比另外一位小朋友的分数多8分时,就停止本轮游戏,并判定得分高的小朋友获胜.现假设“甲小朋友能正确完成一次游戏中的指令动作的概率为α,乙小朋友能正确完成一次游戏中的指令动作的概率为β”,一次游戏中甲小朋友的得分记为X.
(1)求X的分布列;
(2)若甲小朋友、乙小朋友在一轮游戏开始时都赋予4分,pi(i=0,1,…,8)表示“甲小朋友的当前累计得分为i时,本轮游戏甲小朋友最终获胜”的概率,则P0=0,p8=1,pi=api﹣1+bpi+cpi+1(i=1,2,…,7),其中a=P(X=﹣1),b=P(X=0),c=P(X=1).假设α=0.5,β=0.8.
①证明:{pi+1﹣pi}(i=0,1,2,…,7)为等比数列;
②求p4,并根据p4的值说明这种游戏方案是否能够充分验证“甲小朋友能正确完成一次游戏中的指令动作的概率为0.5,乙小朋友能正确完成一次游戏中的指令动作的率为0.8”的假设.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,右焦点到直线
,右焦点到直线![]() 的距离为3.
的距离为3.
(1)求椭圆E的标准方程;
(2)过点A作两条互相垂直的直线![]() ,
,![]() 分别交椭圆于M,N两点,求证:直线MN恒过定点
分别交椭圆于M,N两点,求证:直线MN恒过定点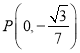 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为2的菱形![]() 中,
中,![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起到
折起到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ⊥平面
⊥平面![]() ,且
,且![]() ,如图2.
,如图2.
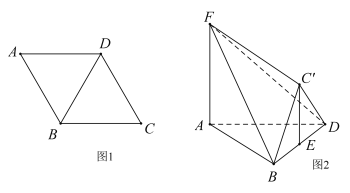
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成角的余弦值;
所成角的余弦值;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ⊥平面
⊥平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—5: 不等式选讲
已知函数f(x)=![]() 的定义域为R.
的定义域为R.
(Ⅰ)求实数m的取值范围;
(Ⅱ)若m的最大值为n,当正数a,b满足![]() =n时,求7a+4b的最小值.
=n时,求7a+4b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校要在一条水泥路边安装路灯,其中灯杆的设计如图所示,AB为地面,CD,CE为路灯灯杆,CD⊥AB,∠DCE=![]() ,在E处安装路灯,且路灯的照明张角∠MEN=
,在E处安装路灯,且路灯的照明张角∠MEN=![]() .已知CD=4m,CE=2m.
.已知CD=4m,CE=2m.
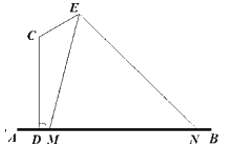
(1)当M,D重合时,求路灯在路面的照明宽度MN;
(2)求此路灯在路面上的照明宽度MN的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建极坐标系,直线
轴的非负半轴为极轴建极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(Ⅰ)求![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)射线![]() 与圆C的交点为
与圆C的交点为![]() 与直线
与直线![]() 的交点为
的交点为![]() ,求
,求![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
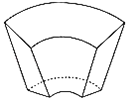
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有曲池,上中周二丈,外周四丈,广一丈,下中周一丈四尺,外周二丈四尺,广五尺,深一丈,问积几何?”其意思为:“今有上下底面皆为扇形的水池,上底中周2丈,外周4丈,宽1丈;下底中周1丈4尺,外周长2丈4尺,宽5尺;深1丈.问它的容积是多少?”则该曲池的容积为( )立方尺(1丈=10尺,曲池:上下底面皆为扇形的土池,其容积公式为![]() [(2×上宽+下宽)
[(2×上宽+下宽)![]() (2×下宽+上宽)
(2×下宽+上宽)![]() ]×深)
]×深)
A.![]() B.1890C.
B.1890C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com