练习册

  • 练习册
  • 试题
    精英家教网 > 高中物理 > 题目详情
    1．水平恒力F作用于放在光滑水平面上质量为m的物体上，使m沿力的方向运动的位移为s，此时力F做功大小为W1；若使水平恒力F作用于放在粗糙水平面上的质量为2m的物体上，使其沿力的方向运动的位移也为s，此时F做功大小为W2，则比较W1与W2的大小为（　　）
    A．W1＞W2B．W1=W2C．W1＜W2D．无法判断

    分析 本题是对功的公式的直接应用，明确功W=FL，即功只取决于力和力的方向上发生的位移．

    解答 解：根据恒力做功的公式W=FL可知，在两次拉物体运动的过程中，拉力的大小相同，物体运动的位移也相等，
    所以两次拉力做的功相同，所以B正确．
    故选：B．

    点评 恒力做功，根据功的公式直接计算即可，要注意准确掌握功的定义，明确功与物体的运动状态无关．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中物理 来源： 题型：多选题

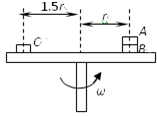    3．如图，叠放在水平转台上的物体A、B、C能随转台一起以角速度ω匀速转动，A、B、C的质量分别为3m、2m、m，A与B、B和C与转台间的最大摩擦因数都为μ，A B和C离转台中心的距离分别为r和1.5r．下列说法正确的是（　　）
    A．B对A的摩擦力一定为3μmg
    B．B对A的摩擦力一定为3m rω2
    C．要使AB和C在转台上都不滑动，转台的角速度一定满足：ω≤$\sqrt{\frac{μg}{r}}$
    D．要使AB和C在转台上都不滑动，转台的角速度一定满足：ω≤$\sqrt{\frac{2μg}{3r}}$

    查看答案和解析>>

    科目：高中物理 来源： 题型：解答题

    4．一传送带装置示意如图，传送带在AB区域是倾斜的，AB的长度l=4.0m、高度差h=0.8m．工作时传送带向上运行的速度保持不变，现将质量均为m=4kg的小货箱（可视为质点）一个接一个在A处从静止释放到传送带上，释放小货箱的时间间隔均为T=2s．小货箱一运动到B处就立刻被取走．传送带由电动机带动，传送带与轮子间无相对滑动，不计轮轴处的摩擦，取g=10m/s2．
    （1）当传送带运行的速度v=2m/s时，小货箱从A处运动到B处所用时间t=3s，求货箱在匀加速运动过程的加速度大小．
    （2）调整传送带运行的速度为另一个更小的值，此后传送带在正常运送小货箱的一段相当长的时间内，小货箱机械能的总增加量与电动机对外做的功之比为17：20，求电动机的平均输出功率$\overline{P}$．

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

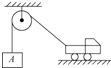    9．如图所示，一辆汽车沿水平地面匀速行驶，通过跨过定滑轮的轻绳将一物体A竖直向上提起，在此过程中，物体A的运动情况是（　　）
    A．加速上升B．减速上升
    C．匀速上升D．以上说法都不正确

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

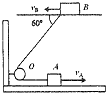    16．如图所示，有两条位于同一竖直平面内的水平轨道，轨道上有两个物体A和B，它们通过一根绕过定滑轮O的不可伸长的轻绳相连接，物体B以vB=10m/s匀速运动，在绳子与轨道α=60°角时，物体A的速度大小vA为：（　　）
    A．5m/sB．5$\sqrt{3}$m/sC．20m/sD．10m/s

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

    6．太阳系中有一颗绕太阳公转的行星，距太阳的平均距离是地球到太阳平均距离的4倍，则该行星绕太阳公转的周期是（　　）
    A．2年B．4年C．8年D．10年

    查看答案和解析>>

    科目：高中物理 来源： 题型：多选题

    13．如图所示，甲从高h处以速度v1平抛小球A，乙同时从地面以初速度V2竖直上抛小球B，在B尚未到达最高点之前，两球在空中相遇，则（　　）
    A．两球相遇时间$t=\frac{h}{v_2}$B．抛出前两球的水平距离$s=\frac{{{v_1}h}}{v_2}$
    C．相遇时A球的速率为$\frac{gh}{v_2}$D．若v2=$\sqrt{gh}$，则两球相遇在$\frac{h}{2}$

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

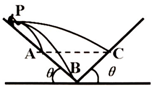    10．如图，在某一峡谷的两侧存在与水平面成相同角度的山坡，某人站在左侧山坡上的P点向对面山坡上水平抛出三个质量不等的石块，分别落在A、B、C三处，不计空气阻力，A、C两处在同一水平面上，则下列说法正确的是（　　）
    A．落在C处的石块在空中运动的时间最长
    B．落在A、B两处的石块落地速度方向相同
    C．落在A、B、C三处的石块落地速度方向相同
    D．落在B、C两处的石块落地速度大小一定不同

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

    11．为了确定某星球的密度与地球密度的关系，宇航员在该星球表面做了一些测试，若测得该星球的自转周期为T，一探测器在该星球两极处所受的重力为P，在该星球赤道处所受的重力为kP（k＜1），假设该星球和地球均是质量分布均匀的球体，一卫星在地球表面附近绕地球做圆周运动的周期为nT（n＞1），则该星球密度与地球密度的比值为（　　）
    A．$\frac{{n}^{2}}{1-k}$B．$\frac{{n}^{2}}{1+k}$C．$\frac{n}{1-k}$D．$\frac{n}{1+k}$

    查看答案和解析>>

    同步练习册答案