
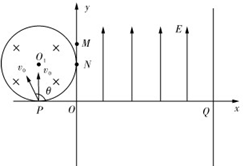
 如图所示,在直角坐标系xOy的第一象限区域中,有沿y轴正方向的匀强电场,电场强度的大小为E=kv0,在第二象限内有一半径为R=b的圆形区域磁场,圆形磁场的圆心O1坐标为(-b,b),与坐标轴分别相切于P点和N点,磁场方向垂直纸面向里,在x=3b处垂直于x轴放置一平面荧光屏,与x轴交点为Q,大量的电子以相同的速率在纸面内从P点进入圆形磁场,电子的速度方向在与x轴正方向成θ角的范围内,其中沿y轴正方向的电子经过磁场到达N点,速度与x轴正方向成θ角的电子经过磁场到达M点且M点坐标为(0,1.5b),忽略电子间的相互作用力,不计电子的重力,电子的比荷为$\frac{e}{m}$=$\frac{{v}_{0}}{kb}$,求:
如图所示,在直角坐标系xOy的第一象限区域中,有沿y轴正方向的匀强电场,电场强度的大小为E=kv0,在第二象限内有一半径为R=b的圆形区域磁场,圆形磁场的圆心O1坐标为(-b,b),与坐标轴分别相切于P点和N点,磁场方向垂直纸面向里,在x=3b处垂直于x轴放置一平面荧光屏,与x轴交点为Q,大量的电子以相同的速率在纸面内从P点进入圆形磁场,电子的速度方向在与x轴正方向成θ角的范围内,其中沿y轴正方向的电子经过磁场到达N点,速度与x轴正方向成θ角的电子经过磁场到达M点且M点坐标为(0,1.5b),忽略电子间的相互作用力,不计电子的重力,电子的比荷为$\frac{e}{m}$=$\frac{{v}_{0}}{kb}$,求:分析 (1)速度沿y轴正方向的电子经过N点,结合几何关系求解轨道半径;根据牛顿第二定律列式求解磁感应强度;
(2)画出速度与x轴正方向成θ角的电子经过磁场过程的轨迹,结合几何关系确定轨道对应的圆心角;
(3)所有的电子以平行于x轴正方向的速度进入电场中做类似平抛运动,根据类似平抛运动的分运动公式列式求解即可.
解答 解:(1)由于速度沿y轴正方向的电子经过N点,因而电子在磁场中做圆周运动的半径为:r=b
而$e{v_0}B=m\frac{v_0^2}{r}$
联立解得:B=$\frac{m{v}_{0}}{eb}$=k
(2)电子在磁场中做圆周运动的圆心为O',电子离开磁场时的位置为P',连接POP'O'可知该四边形为棱形,由于PO竖直,因而 半径P'O'也为竖直方向,电子离开磁场时速度一定沿x轴正方向.
由右图可知: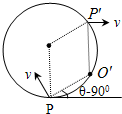
a•sin(θ-90°)+b=1.5b
解得:θ=120°
(3)由(2)可知,所有的电子以平行于x轴正方向的速度进入电场中做类似平抛运动,设电子在电场的运动时间为t,竖直方向位移为y,水平位移为x,
水平:x=v0t 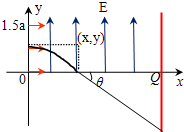
竖直:$y=\frac{1}{2}a{t}^{2}$
eE=ma
vy=at
联立解得:
x=$\sqrt{2by}$
设电子最终打在光屏的最远点距Q点为H.电子射出电场时的夹角为θ有:
tanθ=$\frac{{v}_{y}}{{v}_{0}}$=$\sqrt{\frac{2y}{b}}$
有:H=(3b-x)tanθ=(3$\sqrt{b}$-$\sqrt{2y}$)$\sqrt{2y}$
当$3\sqrt{b}-\sqrt{2y}=\sqrt{2y}$时,即y=$\frac{8}{9}b$时,H有最大值;
由于$\frac{8}{9}b<1.5b$,所以${H}_{max}=\frac{16}{9}b$;
答:(1)圆形磁场的磁感应强度大小为k;
(2)θ角的大小为120°;
(3)电子打到荧光屏上距Q点的最远距离为$\frac{16}{9}b$.
点评 本题关键是明确粒子的受力情况和运动规律,画出临界轨迹,结合牛顿第二定律、类似平抛运动的分运动规律和几何关系分析.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中物理 来源: 题型:选择题
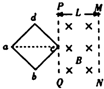 如图所示,宽度为L的匀强磁场的方向垂直纸面向里,正方形线圈abcd的对角线ac与磁场边界PQ垂直,对角线ac的长度也为L,现让正方形线圈abcd以速度v匀速穿过匀强磁场,规定线圈中的电流以顺时针方向为正方向,则在线圈穿过磁场的过程中.电流i随时间t变化的大致情况为( )
如图所示,宽度为L的匀强磁场的方向垂直纸面向里,正方形线圈abcd的对角线ac与磁场边界PQ垂直,对角线ac的长度也为L,现让正方形线圈abcd以速度v匀速穿过匀强磁场,规定线圈中的电流以顺时针方向为正方向,则在线圈穿过磁场的过程中.电流i随时间t变化的大致情况为( )| A. | 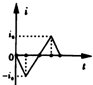 | B. | 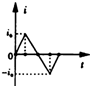 | C. | 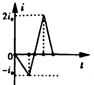 | D. | 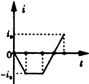 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,打点计时器固定在轨道上端,纸带穿过打点计时器与小车相连,平衡好摩擦力后接通电源,打点计时器工作,轻推小车使之匀速下滑(车轮不打滑),纸带上留下清晰的点迹.
如图所示,打点计时器固定在轨道上端,纸带穿过打点计时器与小车相连,平衡好摩擦力后接通电源,打点计时器工作,轻推小车使之匀速下滑(车轮不打滑),纸带上留下清晰的点迹.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
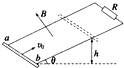 如图所示,间距为L米的光滑平等金属轨道上端用电阻R相连,其平面与水平面成θ角,整个装置处于磁感应强度为B匀强磁场中,磁场方向垂直轨道平面向上,质量为m,电阻为r的金属杆ab(长度略大于L),以初速度v0从轨道底端向上滑行,滑行到距底端高h的位置后又返回到底端,运动过程中,金属杆始终与导轨垂直且接触良好,不计金属轨道的电阻,已知重力加速度为g,则以下说法正确的是( )
如图所示,间距为L米的光滑平等金属轨道上端用电阻R相连,其平面与水平面成θ角,整个装置处于磁感应强度为B匀强磁场中,磁场方向垂直轨道平面向上,质量为m,电阻为r的金属杆ab(长度略大于L),以初速度v0从轨道底端向上滑行,滑行到距底端高h的位置后又返回到底端,运动过程中,金属杆始终与导轨垂直且接触良好,不计金属轨道的电阻,已知重力加速度为g,则以下说法正确的是( )| A. | 杆ab先匀减速上滑,之后匀加速下滑,且上滑过程的加速度大于下滑过程的加速度 | |
| B. | 杆ab运动过程中安培力做功的功率等于电阻R的热功率 | |
| C. | 杆ab上滑过程中通过R的电荷量与下滑过程中通过R的电荷量相等 | |
| D. | 杆ab上滑到最高点的过程中电阻R上产生的焦耳热等于$\frac{R}{R+r}$($\frac{1}{2}$mv02-mgh) |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
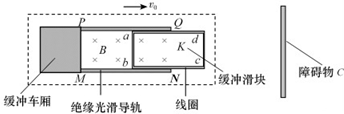
| A. | 线圈中的感应电流沿逆时针方向(俯视),最大感应电流为$\frac{BL{v}_{0}}{R}$ | |
| B. | 线圈对电磁铁的作用力使缓冲车厢减速运动,从而实现缓冲 | |
| C. | 此过程中,线圈abcd产生的焦耳热为Q=$\frac{1}{2}$mv02 | |
| D. | 此过程中,通过线圈abcd的电荷量为q=$\frac{B{L}^{2}}{R}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
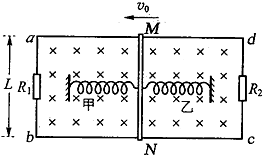 如图所示,abcd为固定的水平光滑矩形金属导轨,导轨间距为L,左右两端接有定值电阻R1和R2,R1=R2=R,整个装置处于磁感应强度大小为B、方向竖直向下的匀强磁场中.质量为m的导体棒MN放在导轨上,棒始终与导轨垂直且接触良好,不计导轨与棒的电阻.两根相同的轻质弹簧甲和乙一端固定,另一端同时与棒的中点连接.初始时刻,两根弹簧恰好处于原长状态,棒获得水平向左的初速度v0,第一次运动至最右端的过程中R1产生的电热为Q,下列说法中正确的是( )
如图所示,abcd为固定的水平光滑矩形金属导轨,导轨间距为L,左右两端接有定值电阻R1和R2,R1=R2=R,整个装置处于磁感应强度大小为B、方向竖直向下的匀强磁场中.质量为m的导体棒MN放在导轨上,棒始终与导轨垂直且接触良好,不计导轨与棒的电阻.两根相同的轻质弹簧甲和乙一端固定,另一端同时与棒的中点连接.初始时刻,两根弹簧恰好处于原长状态,棒获得水平向左的初速度v0,第一次运动至最右端的过程中R1产生的电热为Q,下列说法中正确的是( )| A. | 初始时刻棒所受安培力的大小为$\frac{{B}^{2}{L}^{2}{v}_{0}}{R}$ | |
| B. | 棒第一次回到初始位置的时刻,R2的电功率为$\frac{{B}^{2}{L}^{2}{{v}_{0}}^{2}}{R}$ | |
| C. | 棒第一次到达最右端的时刻,两根弹簧具有弹性势能的总量为$\frac{1}{2}$mv${\;}_{0}^{2}$-Q | |
| D. | 从初始时刻至棒第一次到达最左端的过程中,整个回路产生的电热大于$\frac{2Q}{3}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
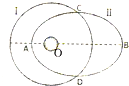 如图所示,曲线Ⅰ是绕地球做圆周运动卫星1的轨道示意图,其半径为R;曲线Ⅱ是绕地球做椭圆运动卫星2的轨道的示意图,O点为地球球心,AB为椭圆的长轴,两轨道和地心都在同一平面内,己知在两轨道上运动的卫星的周期相等,万有引力常量为G,地球质量为M,下列说法正确的是( )
如图所示,曲线Ⅰ是绕地球做圆周运动卫星1的轨道示意图,其半径为R;曲线Ⅱ是绕地球做椭圆运动卫星2的轨道的示意图,O点为地球球心,AB为椭圆的长轴,两轨道和地心都在同一平面内,己知在两轨道上运动的卫星的周期相等,万有引力常量为G,地球质量为M,下列说法正确的是( )| A. | 椭圆轨道的长轴AB长度为R | |
| B. | 若OA=0.5R,则卫星在B点的速率vB<$\sqrt{\frac{2GM}{3R}}$ | |
| C. | 在Ⅰ轨道上卫星1的速率为v0,在Ⅱ轨道的卫星2在B点的速率为vB,则v0<vB | |
| D. | 两颗卫星运动到C点时,卫星1和卫星2的加速度不同 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 天然放射现象的发现揭示了原子核有复杂的结构 | |
| B. | 氢原子从n=3的能级向低能级跃迁时只会辐射出两种不同频率的光 | |
| C. | 比结合能大的原子核分解成比结合能小的原子核时要吸收能量 | |
| D. | 放射性元素每经过一个半衰期,其质量减少一半 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com