
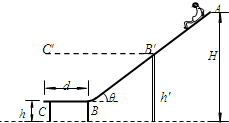
 水上滑梯可简化成如图所示的模型:倾角为θ=37°斜滑道AB和水平滑道BC平滑连接,起点A距水面的高度H=7.0m,BC长d=2.0m,端点C距水面的高度h=1.0m.一质量m=50kg的运动员从滑道起点A点无初速地自由滑下,运动员与AB、BC间的动摩擦因数均为μ=0.10,(cos37°=0.8,sin37°=0.6,运动员在运动过程中可视为质点)求:
水上滑梯可简化成如图所示的模型:倾角为θ=37°斜滑道AB和水平滑道BC平滑连接,起点A距水面的高度H=7.0m,BC长d=2.0m,端点C距水面的高度h=1.0m.一质量m=50kg的运动员从滑道起点A点无初速地自由滑下,运动员与AB、BC间的动摩擦因数均为μ=0.10,(cos37°=0.8,sin37°=0.6,运动员在运动过程中可视为质点)求: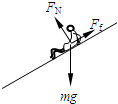
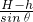 )+μmgd=μmg[d+(H-h)cotθ]=500J
)+μmgd=μmg[d+(H-h)cotθ]=500J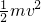 ,
, ,得
,得 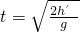
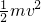 ,
,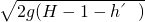
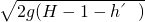 ?
?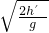 =
=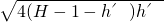
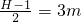 时,水平位移最大
时,水平位移最大 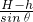 )+μmgd=μmg[d+(H-h)cotθ].根据动能定理求解到达C点时速度的大小υ;
)+μmgd=μmg[d+(H-h)cotθ].根据动能定理求解到达C点时速度的大小υ;

科目:高中物理 来源: 题型:
 水上滑梯可简化成如图所示的模型,斜槽AB和水平槽BC平滑连接,斜槽AB的竖直高度H=6.0m,倾角θ=37°.水平槽BC长d=2.0m,BC面与水面的距离h=0.80m,人与AB、BC间的动摩擦因数均为μ=0.10.取重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6.一小朋友从滑梯顶端A点无初速地自由滑下,求:
水上滑梯可简化成如图所示的模型,斜槽AB和水平槽BC平滑连接,斜槽AB的竖直高度H=6.0m,倾角θ=37°.水平槽BC长d=2.0m,BC面与水面的距离h=0.80m,人与AB、BC间的动摩擦因数均为μ=0.10.取重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6.一小朋友从滑梯顶端A点无初速地自由滑下,求:查看答案和解析>>
科目:高中物理 来源: 题型:
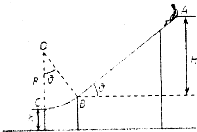 水上滑梯可简化成如图所示的模型,斜槽AB和光滑圆弧槽BC平滑连接,斜槽AB的竖直高度H=6.0m,倾角θ=37°.圆弧BC半径R=3.0m,末端C点的切线水平;C点与水平面的距离h=0.80m,人与AB间的动摩擦因数为μ=0.2.取重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6.一个质量m=30kg的小朋友从滑梯顶端A点无初速地自由滑下,求:
水上滑梯可简化成如图所示的模型,斜槽AB和光滑圆弧槽BC平滑连接,斜槽AB的竖直高度H=6.0m,倾角θ=37°.圆弧BC半径R=3.0m,末端C点的切线水平;C点与水平面的距离h=0.80m,人与AB间的动摩擦因数为μ=0.2.取重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6.一个质量m=30kg的小朋友从滑梯顶端A点无初速地自由滑下,求:查看答案和解析>>
科目:高中物理 来源: 题型:
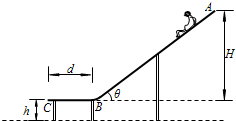 水上滑梯可简化成如图所示的模型,斜槽AB和水平槽BC平滑连接,斜槽AB的竖直高度H=6.0m,倾角θ=37°.水平槽BC长d=2.0m,BC面与水面的距离h=0.80m,人与AB、BC间的动摩擦因数均为μ=0.10.取重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6.一小朋友从滑梯顶端A点无初速地自由滑下,求:
水上滑梯可简化成如图所示的模型,斜槽AB和水平槽BC平滑连接,斜槽AB的竖直高度H=6.0m,倾角θ=37°.水平槽BC长d=2.0m,BC面与水面的距离h=0.80m,人与AB、BC间的动摩擦因数均为μ=0.10.取重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6.一小朋友从滑梯顶端A点无初速地自由滑下,求:查看答案和解析>>
科目:高中物理 来源: 题型:
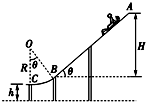 水上滑梯可简化成如图所示的模型,斜槽AB和光滑圆弧槽BC平滑连接.斜槽AB的竖直高度差H=0.6m,倾角θ=37°;圆弧槽BC的半径R=3.0m,末端C点的切线水平;C点与水面的距离h=0.80m.人与AB间的动摩擦因数μ=0.2,取重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6.一个质量m=30kg的小朋友从滑梯顶端A点无初速度地自由滑下,不计空气阻力,求:
水上滑梯可简化成如图所示的模型,斜槽AB和光滑圆弧槽BC平滑连接.斜槽AB的竖直高度差H=0.6m,倾角θ=37°;圆弧槽BC的半径R=3.0m,末端C点的切线水平;C点与水面的距离h=0.80m.人与AB间的动摩擦因数μ=0.2,取重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6.一个质量m=30kg的小朋友从滑梯顶端A点无初速度地自由滑下,不计空气阻力,求:查看答案和解析>>
科目:高中物理 来源: 题型:
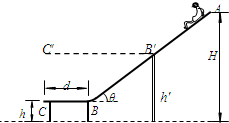 水上滑梯可简化成如图所示的模型:倾角为θ=37°斜滑道AB和水平滑道BC平滑连接,起点A距水面的高度H=7.0m,BC长d=2.0m,端点C距水面的高度h=1.0m.一质量m=50kg的运动员从滑道起点A点无初速地自由滑下,运动员与AB、BC间的动摩擦因数均为μ=0.10,(cos37°=0.8,sin37°=0.6,运动员在运动过程中可视为质点)求:
水上滑梯可简化成如图所示的模型:倾角为θ=37°斜滑道AB和水平滑道BC平滑连接,起点A距水面的高度H=7.0m,BC长d=2.0m,端点C距水面的高度h=1.0m.一质量m=50kg的运动员从滑道起点A点无初速地自由滑下,运动员与AB、BC间的动摩擦因数均为μ=0.10,(cos37°=0.8,sin37°=0.6,运动员在运动过程中可视为质点)求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com