Question

4．如图倾角为θ的光滑斜面与粗糙的水平面相连，在Q点正上方R处的O点有垂直于纸面的水平轴，长为R的轻杆可绕轴在竖直面内无摩擦的转动，杆的下端固定一质量为m的小球B，B与地面刚好无压力．质量也为m的小滑块A从斜面上高为H=1.6m的位置自由滑下，在P点滑块的速度大小不受影响，到Q点后与B发生碰撞（已知A、B间的碰撞为水平方向的弹性碰撞）．已知A与水平面的摩擦因数为μ=0.25，P、Q间的距离为S=1.0m．
求：（1）A与B刚碰撞前的瞬间A的速度的大小．
（2）求滑块A最终所停位置距离Q多远．

Answer 1

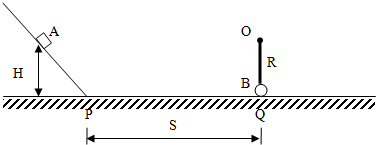
分析 （1）A到达Q的过程中，重力和阻力对A做功，由功能关系即可求出A的速度；
（2）分析B过最高点的条件，然后根据机械能守恒，得出B在最低点的速度的特点，最后结合弹性碰撞的特点以及功能关系即可求出．

解答 解：（1）A到达Q的过程中，重力和阻力对A做功，得：$mgH-μmgS=\frac{1}{2}m{v}_{0}^{2}$
所以：${v}_{0}=3\sqrt{3}$m/s
（2）由于B与A的质量相等，A与B碰撞的过程是弹性碰撞，根据弹性碰撞的特点可知，质量相等的两个物体在碰撞后交换速度，所以碰撞后A的速度变成0，而B的速度变成3$\sqrt{3}$m/s．
若B能恰好经过最高点，则在最高点的速度恰好为0，根据机械能守恒得最低点的速度满足：
-mg•2R=$0-\frac{1}{2}m{v}_{B}^{2}=-\frac{1}{2}m{v}_{0}^{2}$
代入数据得：R=0.675 m
讨论：
Ⅰ、若杆的长度小于0.675m，则小球B能越过最高点，继续沿逆时针方向转到B，然后与A发生弹性碰撞，再次交换速度．之后A继续以速度3$\sqrt{3}$m/s向右运动到停止，由动能定理得：$-μmgx=0-\frac{1}{2}m{v}_{0}^{2}$
所以x=5.4m
Ⅱ、若杆的长度大于0.675m，则小球B不能越过最高点，则将沿顺时针方向返回到B，然后与A发生弹性碰撞，再次交换速度．之后A继续以速度3$\sqrt{3}$m/s向左运动到停止，由动能定理得：$-μmgx=0-\frac{1}{2}m{v}_{0}^{2}$
由于：x＞S，所以A将回到P点，然后沿斜面向上运动，到达最高点后再次返回P点，再向右运动直到与Q发生第三次的碰撞．由于A再次在水平面上运动的过程中摩擦力继续做功，可知B仍然不能到达最高点，仍然是再沿顺时针方向返回…
由此可知，A将在PQ之间以及斜面上做往返运动，一直到停止上，运动的总路程为5.4m．
由：5.4m=1m×5+0.4m
可知A将在从P向Q运动的过程中停止，此时距离Q点的路程为：L=1m-0.4m=0.6m
答：（1）A与B刚碰撞前的瞬间A的速度的大小是$3\sqrt{3}$m/s；
（2）当R＞0.675m时，A将停在Q的左侧距Q 0.6米处；当R≤0.675m时，A将停在Q的右侧距Q 5.4米处．

点评 该题结合弹性碰撞的情况，考查对功能关系的应用能力，在解答的过程中要注意B做圆周运动的过程中可能能通过最高点，有可能不会通过最高点，要讨论，不能遗漏．