
 ��ͼ��ʾ��ˮƽ�����Բ�δų���������ֱ�߽�MN������C�㣬�ų��뾶ΪR��C����ų�Բ��O�ȸߣ��߽�PQ��ӫ����GH����MNƽ�У���MN��PQ֮����Ϊ$\frac{\sqrt{3}}{2}$R��PQ��GH֮��ļ��ΪR����PQ��GH�������ֱ���µ���ǿ�糡���糡ǿ��E=$\frac{m{v}_{0}^{2}}{2qR}$���ִ�O�����·���A��ͬʱ��ֱ�ų���������������ͬ�Ĵ�������1��2�����ǵ�����Ϊm������Ϊ+q���ٶȴ�С��Ϊv0������1���ٶȷ���ָ��O�㣬����2���ٶȷ�����AO��300�н�б�����Ϸ�������1ǡ�ܴ�C������ų���������Ϊ�ʵ㣬��ͼʾƽ�����˶�����������ֲ��䣬���ƿ������������������Ա�ԵЧӦ��
��ͼ��ʾ��ˮƽ�����Բ�δų���������ֱ�߽�MN������C�㣬�ų��뾶ΪR��C����ų�Բ��O�ȸߣ��߽�PQ��ӫ����GH����MNƽ�У���MN��PQ֮����Ϊ$\frac{\sqrt{3}}{2}$R��PQ��GH֮��ļ��ΪR����PQ��GH�������ֱ���µ���ǿ�糡���糡ǿ��E=$\frac{m{v}_{0}^{2}}{2qR}$���ִ�O�����·���A��ͬʱ��ֱ�ų���������������ͬ�Ĵ�������1��2�����ǵ�����Ϊm������Ϊ+q���ٶȴ�С��Ϊv0������1���ٶȷ���ָ��O�㣬����2���ٶȷ�����AO��300�н�б�����Ϸ�������1ǡ�ܴ�C������ų���������Ϊ�ʵ㣬��ͼʾƽ�����˶�����������ֲ��䣬���ƿ������������������Ա�ԵЧӦ������ ������Բ�δų�������������Բ���˶����漰��Բ�ཻ�ļ���֪ʶ�����ܿ�����ѧӦ��������
��1����������1��A����AO���룬��C�����������֪�����ӵĹ���뾶ΪR���Ӷ���ôŸ�Ӧǿ�ȣ�
��2������2ֻ�����䷽��ͬ�����ݰ뾶��ͬ����Բ�ཻ�����ʵõ�������2���䷽��ǡ��MN��ֱ���������MN��ˮƽ����ΪR-Rcos30�㣬����ˮƽ����ֱ���˶���λ�Ƴ����ٶȵõ��ڶ��ε�ʱ�䣮ˮƽ����糡��������ƽ���˶�������ˮƽλ�����ʱ�䣮
��� �⣺��1������1��A�����C��������ɼ��ι�ϵ�õ�����1�ڴų�����������Բ���˶��İ뾶��
r1=R ��
������1�ڴų����У�
$q{v}_{0}B=\frac{{{mv}_{0}}^{2}}{{r}_{1}}$ ��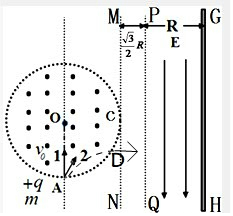
�����ã�$B=\frac{m{v}_{0}}{qR}$��
��2������2��AO��30�����䣬Ҳ���뾶Ϊr2=R������Բ���˶���
�����ཻԲ������֪������2ת��60���D��������ڴų�������ʱ��Ϊ��
${t}_{1}=\frac{1}{6}T=\frac{��R}{3{v}_{0}}$
��������2��ʼ����ֱ�����30�����䣬��ת��60�㣬���뿪�ų�ʱ�ٶȷ���ǡ��MN��ֱ����ô��MP֮��������ֱ���˶���ʱ��Ϊ��
${t}_{2}=\frac{MP+R-Rcos30��}{{v}_{0}}=\frac{R}{{v}_{0}}$
����糡������ƽ���˶���ʱ��Ϊ
${t}_{3}=\frac{R}{{v}_{0}}$
������ʱ��Ϊ$t={t}_{1}+{t}_{2}+{t}_{3}=\frac{��+6}{3{v}_{0}}R$
�𣺣�1��Բ�δų��ĴŸ�Ӧǿ��Ϊ$\frac{m{v}_{0}}{qR}$��
��2������2�ӽ���ų���ӫ��������ʱ��Ϊ$\frac{��+6}{3{v}_{0}}R$
���� ������ѵ���������2����ų�����ij�������⣬�漰���ཻԲ�����ʶ������״��������뿪�ų���ˮƽ����ֱ���˶��˶���λ�ƣ����ֿ��쵽����֪ʶ�������ڵ糡�е��˶�������ˮƽλ�ƾͿ����ʱ�䣮


 A�ӽ��� ϵ�д�
A�ӽ��� ϵ�д� ȫ�Ų��Ծ�ϵ�д�
ȫ�Ų��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | 4N | B�� | 8N | C�� | 10 N | D�� | 15 N |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ����ֻͬ���ĵ��ɳ�ÿֻ����0.1N���¶˵Ĺҹ��������Բ��ƣ��ס����ҡ����ҡ����ҡ������ҵ��·�������0.2N�����룬��ס��ҵ��ɳӵĶ����ֱ�Ϊ��������
��ͼ��ʾ����ֻͬ���ĵ��ɳ�ÿֻ����0.1N���¶˵Ĺҹ��������Բ��ƣ��ס����ҡ����ҡ����ҡ������ҵ��·�������0.2N�����룬��ס��ҵ��ɳӵĶ����ֱ�Ϊ��������| A�� | 0.2 N��0.3 N | B�� | 0.3 N��0.2 N | C�� | 0.3 N��0.3 N | D�� | 0.4 N��0.3 N |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 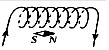 | B�� | 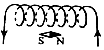 | C�� | 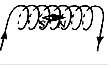 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
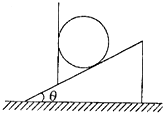 һ������Ϊm�ľ�������������Ϊ�ȵĹ⻬б���ϣ�����б����һ����ֱ��ˮƽ��Ĺ⻬���嵲ס������ƽ��״̬�����б��������֧������Ϊ���٣�
һ������Ϊm�ľ�������������Ϊ�ȵĹ⻬б���ϣ�����б����һ����ֱ��ˮƽ��Ĺ⻬���嵲ס������ƽ��״̬�����б��������֧������Ϊ���٣��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
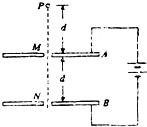 ��ͼ��ʾ��A��BΪƽ�н����壬�������Ϊd���ֱ����Դ����������������������һС��M��N������һ�����ʵ㣬��A���Ϸ����Ϊd��P���ɾ�ֹ�������䣨P��M��N��ͬһ��ֱ���ϣ��������������Բ��ƣ�����N��ʱ�ٶ�ǡ��Ϊ�㣮Ȼ����ԭ·���أ��������������ĵ�ѹ���䣬����ȷ���ǣ�������
��ͼ��ʾ��A��BΪƽ�н����壬�������Ϊd���ֱ����Դ����������������������һС��M��N������һ�����ʵ㣬��A���Ϸ����Ϊd��P���ɾ�ֹ�������䣨P��M��N��ͬһ��ֱ���ϣ��������������Բ��ƣ�����N��ʱ�ٶ�ǡ��Ϊ�㣮Ȼ����ԭ·���أ��������������ĵ�ѹ���䣬����ȷ���ǣ�������| A�� | �ʵ��P��N�����У��������ܵļ�С�����ڵ����ܵ������� | |
| B�� | �ʵ��ڵ糡���˶�ʱ���ܵ糡���Ĵ�СΪ���������� | |
| C�� | ����A������ƽ��һС�ξ��룬�ʵ���P������������ܷ��� | |
| D�� | ����B������ƽ��һС�ξ��룬�ʵ���P�������������N�������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
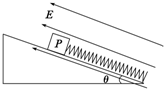 ��ͼ��ʾ��һ��Ե�ᵯ�ɵ��¶˹̶���б��ˣ��϶�����һ������Ĺ⻬����P�����������ռ��������б�����ϵ���ǿ�糡�����Ϊ�ȵĹ⻬��Եб��̶���ˮƽ�����ϣ���ʼʱ���ɴ���ԭ��״̬����鴦��ƽ��״̬���ָ�����һ��б�����µij��ٶ�v�����鵽��͵�ʱ�����ɵ�ѹ����Ϊx��������ʼ�մ��ڵ������ڣ��ӻ����ó��ٶ�v ֱ��������͵�Ĺ����У�����˵����ȷ���ǣ�������
��ͼ��ʾ��һ��Ե�ᵯ�ɵ��¶˹̶���б��ˣ��϶�����һ������Ĺ⻬����P�����������ռ��������б�����ϵ���ǿ�糡�����Ϊ�ȵĹ⻬��Եб��̶���ˮƽ�����ϣ���ʼʱ���ɴ���ԭ��״̬����鴦��ƽ��״̬���ָ�����һ��б�����µij��ٶ�v�����鵽��͵�ʱ�����ɵ�ѹ����Ϊx��������ʼ�մ��ڵ������ڣ��ӻ����ó��ٶ�v ֱ��������͵�Ĺ����У�����˵����ȷ���ǣ�������| A�� | ��������ܵ����������ڻ����������ܵļ����� | |
| B�� | ���鵽����͵�Ĺ����У��˷����ɵ�������$\frac{1}{2}$mv2 | |
| C�� | ���鶯�ܵı仯�����ڵ糡�������������Ĵ����� | |
| D�� | ������ļ��ٶ����ʱ������͵�����ɵ�ϵͳ��е����С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
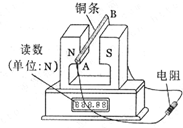 ��ͼ��ʾΪһ�ֿɲ����Ÿ�Ӧǿ�ȵ�ʵ��װ�ã���������ˮƽ���õĵ��Ӳ������ϣ�����֮��Ĵų�����Ϊˮƽ��ǿ�ų�����������ų���Ӱ��ɺ��Բ��ƣ���ʱ���Ӳ����Ƶ�ʾ��ΪG1����һֱͭ��ABˮƽ�Ҵ�ֱ�ڴų��������ڴų��У�����ͨ��������һ�������ӳɱպϻ�·����ʱ���Ӳ����Ƶ�ʾ��ΪG2����ʹͭ������ֱ���µĺ㶨����v�ڴų����˶�����ʱ���Ӳ����Ƶ�ʾ��ΪG3�����ͭ������ǿ�ų��еij���ΪL����·����ֵΪR��ͭ��ʼ��δ������Ӵ�������˵����ȷ���� ��������
��ͼ��ʾΪһ�ֿɲ����Ÿ�Ӧǿ�ȵ�ʵ��װ�ã���������ˮƽ���õĵ��Ӳ������ϣ�����֮��Ĵų�����Ϊˮƽ��ǿ�ų�����������ų���Ӱ��ɺ��Բ��ƣ���ʱ���Ӳ����Ƶ�ʾ��ΪG1����һֱͭ��ABˮƽ�Ҵ�ֱ�ڴų��������ڴų��У�����ͨ��������һ�������ӳɱպϻ�·����ʱ���Ӳ����Ƶ�ʾ��ΪG2����ʹͭ������ֱ���µĺ㶨����v�ڴų����˶�����ʱ���Ӳ����Ƶ�ʾ��ΪG3�����ͭ������ǿ�ų��еij���ΪL����·����ֵΪR��ͭ��ʼ��δ������Ӵ�������˵����ȷ���� ��������| A�� | G1��G2��G3 | B�� | G1=G2��G3 | C�� | B=$\frac{1}{L}$$\sqrt{\frac{��{G}_{3}-{G}_{1}��R}{v}}$ | D�� | B=$\frac{1}{L}$$\sqrt{\frac{��{G}_{3}-{G}_{2}��R}{v}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
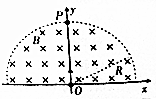 ��ͼ��ʾ����ֱ������ϵxOy����ƽ���ڣ��������ԭ��OΪԲ�ġ��뾶ΪR�İ�Բ�������ڣ����ڷ���ֱֽ������Ĵ�СΪB����ǿ�ų��ʹ�С�������δ֪����ǿ�糡��t=0ʱ����ԭ��O��+y��������һ�����硢�������Ƶ����ӣ�������ǡ��y��������ֱ���˶�����t=t0ʱ�̴�y���ϵ�P�������Բ������
��ͼ��ʾ����ֱ������ϵxOy����ƽ���ڣ��������ԭ��OΪԲ�ġ��뾶ΪR�İ�Բ�������ڣ����ڷ���ֱֽ������Ĵ�СΪB����ǿ�ų��ʹ�С�������δ֪����ǿ�糡��t=0ʱ����ԭ��O��+y��������һ�����硢�������Ƶ����ӣ�������ǡ��y��������ֱ���˶�����t=t0ʱ�̴�y���ϵ�P�������Բ�������鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com