
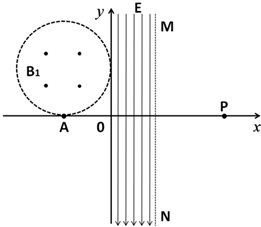
 ��ͼ��ʾ���ڶ����ޣ��뾶Ϊr��Բ�������ڴ��ڷ���ֱֽ���������ǿ�ų����ų��߽�ǡ���������������У�x�����е�A����һ����Դ���ܸ���x���Ϸ�����������ȣ���Ϊv������Ϊm������Ϊ+q�����ӣ������������ƣ�Բ������ų��ĴŸ�Ӧǿ��B1=$\frac{mv}{qr}$��y���Ҳ�0��y��r�ķ�Χ�ڴ�����y�Ḻ�������ǿ�糡����֪ij���Ӵ�A����+y��������ų����ٽ�����ǿ�糡���������Ӵӵ糡�ұ߽�MN������ٶȷ�����x���������45���б���£���
��ͼ��ʾ���ڶ����ޣ��뾶Ϊr��Բ�������ڴ��ڷ���ֱֽ���������ǿ�ų����ų��߽�ǡ���������������У�x�����е�A����һ����Դ���ܸ���x���Ϸ�����������ȣ���Ϊv������Ϊm������Ϊ+q�����ӣ������������ƣ�Բ������ų��ĴŸ�Ӧǿ��B1=$\frac{mv}{qr}$��y���Ҳ�0��y��r�ķ�Χ�ڴ�����y�Ḻ�������ǿ�糡����֪ij���Ӵ�A����+y��������ų����ٽ�����ǿ�糡���������Ӵӵ糡�ұ߽�MN������ٶȷ�����x���������45���б���£������� ��1�������ڵ糡������ƽ���˶�������ţ�ٵڶ����ɺͷ�λ�ƹ�ʽ�����ٶȹ�ʽ��ʽ���E��
��2�������ڴų���������Բ���˶�����ţ�ٵڶ����ɵõ��켣�뾶���ɼ��ι�ϵ�����������Ŀ��ȣ��Ӷ����Բ����ǿ�ų�B2����С�뾶��
��3�����ݻ��������ٶȴ�С֮���������ڴų����˶�ʱ�䣮�ɷ��˶���λ�ƹ�ʽ��糡���˶�ʱ�䣮�õ������������˶���ʱ�䣬�������˶��Ĺ������ʱ�䣬�Ӷ��õ���ʱ�䣮
��� �⣺��1���ڵ糡������ƽ���˶�����qE=ma���� a=$\frac{qE}{m}$
����ƽ���˶��Ĺ����У�
x=vt=r
vy=at=$\frac{qE}{m}$•$\frac{r}{v}$=$\frac{qEr}{mv}$
���Ӵӵ糡�ұ߽�MN������ٶȷ�����x���������45��б���£��� vy=v��
������ E=$\frac{m{v}^{2}}{qr}$
��2�������ڴų���������Բ���˶�����ţ�ٵڶ����ɵ�
qVB1=m$\frac{{v}^{2}}{R}$��B1=$\frac{mv}{qr}$���� R=r
��Ϊ�ų��뾶��켣�뾶��ͬ�����������뿪�ų�����ٶȷ������+x����
���������Ӵ�����ǿ�糡���ٶ�����ƫ���� y=$\frac{1}{2}a{t}^{2}$=$\frac{1}{2}r$�������
�����Ӵ�MN�������ߵ�ΪE����͵�ΪF����EF=2r
�����������Ŀ��� d=$\sqrt{2}$r
Բ����ǿ�ų�B2����С�뾶 rB2=$\frac{\sqrt{2}}{2}$r
��3�������ڴų�B1���˶�ʱ�� t1=$\frac{l}{v}$=$\frac{��r}{2v}$
��������ǿ�糡���˶�ʱ�� t2=$\frac{r}{v}$
���������˶��ٶ� v��=$\sqrt{2}$v
���������˶��ľ��� x3=$\frac{\sqrt{2}}{2}$r
���������˶���ʱ�� t3=$\frac{{x}_{3}}{v��}$=$\frac{r}{2v}$
�����ڴų�B2���˶�ʱ�� t4=$\frac{��r}{4v}$
��������A���˶���x���ϵ�P�����ʱ�� t=t1+t2+t3+t4=$\frac{3r}{2v}$+$\frac{3��r}{4v}$
��
��1����ǿ�糡�ĵ糡ǿ�ȴ�С��$\frac{m{v}^{2}}{qr}$��
��2��Բ����ǿ�ų�B2����С�뾶Ϊ$\frac{\sqrt{2}}{2}$r��
��3��������A���˶���x���ϵ�P�����ʱ��Ϊ$\frac{3r}{2v}$+$\frac{3��r}{4v}$��
���� ������������������������������Բ���˶����ڵ糡������������ƽ���˶������������˶��Ĵ������ɣ�ѧ���˶��ķֽ��뼸�ι�ϵ��Ӧ�ã�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2��n}{Rt}$$\sqrt{\frac{{g}_{0}}{L}}$-R | B�� | $\frac{Rt}{2��n}$$\sqrt{\frac{L}{{g}_{0}}}$-R | C�� | $\frac{2��Rt}{n}$$\sqrt{\frac{L}{{g}_{0}}}$-R | D�� | $\frac{Rt}{2��n}$$\sqrt{\frac{{g}_{0}}{L}}$-R |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
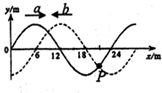 �������Ϊ2cm������24cm�Ͳ���12m/s��г�Შa��b���ֱ���x�����������������t=0ʱ�̵IJ��ֲ���ͼ��ͼ��ʾ��������
�������Ϊ2cm������24cm�Ͳ���12m/s��г�Შa��b���ֱ���x�����������������t=0ʱ�̵IJ��ֲ���ͼ��ͼ��ʾ��������| A�� | ͼ��x=15m�����ʵ��Ǽ�ǿ�� | |
| B�� | ͼ��x=21m����P�ʵ㾭ʱ��t=0.75�����ٶ����ֵ | |
| C�� | �����в��������ܷ����������� | |
| D�� | ��������Ҫ�������Ե������������������ϰ���ijߴ�һ�㲻����2cm |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ̫�������������Ҫ����̫���ڲ�����˾۱� | |
| B�� | ��˾۱����غ��ѱ�����������Ժ˷�Ӧ�����е��������� | |
| C�� | ԭ�Ӻ˵ıȽ����Խ���ʾ��ԭ�Ӻ�Խ���ȶ� | |
| D�� | ʵ�������ֻҪ������ǿ���㹻��һ���ܷ������ЧӦ���� | |
| E�� | ������Ӧ�ù��ЧӦԭ���ƳɵĹ��ת������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
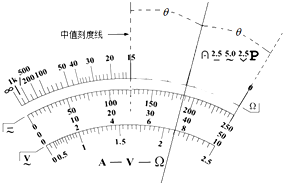 ����һ���õ������ŷķ���ġ�0���̶�������ֵ�̶���֮��Ŀ̶�ģ�������á���100����ŷķ����������淶����ijһ�������R��ָ����ָ��λ���롰0���̶��ߺ���ֵ�̶���ļн���ȣ���ͼ��ʾ����ô������R=500����
����һ���õ������ŷķ���ġ�0���̶�������ֵ�̶���֮��Ŀ̶�ģ�������á���100����ŷķ����������淶����ijһ�������R��ָ����ָ��λ���롰0���̶��ߺ���ֵ�̶���ļн���ȣ���ͼ��ʾ����ô������R=500�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
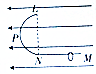 ��ͼ��ʾ����E=75V/m��ˮƽ�������ǿ�糡�У���һ�⻬�İ�Բ�ξ�Ե���LPN��һˮƽ��Ե���MN���ӣ���Բ�����ڵ���ֱƽ����糡��ƽ�У���뾶R=0.40m������PΪLNԲ�����е㣬ֱ��LN��ˮƽ���MN��ֱ������һ�����������q=1��10-3C������m=1.0��10-2kg��С�����ڹ���ϣ��˻���λ��N���Ҳ�x=1.2m���Գ��ٶ�v0����ʼ�˶�����֪С����ˮƽ�����Ķ�Ħ��������=0.25������ǡ���˶���Բ�������ߵ�L��ȡg=10m/s2 ����
��ͼ��ʾ����E=75V/m��ˮƽ�������ǿ�糡�У���һ�⻬�İ�Բ�ξ�Ե���LPN��һˮƽ��Ե���MN���ӣ���Բ�����ڵ���ֱƽ����糡��ƽ�У���뾶R=0.40m������PΪLNԲ�����е㣬ֱ��LN��ˮƽ���MN��ֱ������һ�����������q=1��10-3C������m=1.0��10-2kg��С�����ڹ���ϣ��˻���λ��N���Ҳ�x=1.2m���Գ��ٶ�v0����ʼ�˶�����֪С����ˮƽ�����Ķ�Ħ��������=0.25������ǡ���˶���Բ�������ߵ�L��ȡg=10m/s2 �����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
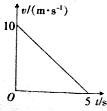 ����Ϊ2kg����������ˮƽ���ϣ����˶�������������F������ˮƽ�����ȱ����˶��������˶���v-tͼ����ͼ��ʾ��������������Ķ�Ħ������Ϊ0.5g��gȡ10m/s2����5s��������Ħ����������Ϊ���٣�
����Ϊ2kg����������ˮƽ���ϣ����˶�������������F������ˮƽ�����ȱ����˶��������˶���v-tͼ����ͼ��ʾ��������������Ķ�Ħ������Ϊ0.5g��gȡ10m/s2����5s��������Ħ����������Ϊ���٣��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com