
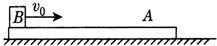
 如图所示,在足够长的光滑水平面上,放置一长为L=1m、质量为m1=0.5kg的木板A,一质量为m2=1kg的小物体B以初速度υ0=4m/s滑上A的上表面,A与B之间的动摩擦因数为μ=0.2,g=10m/s2;
如图所示,在足够长的光滑水平面上,放置一长为L=1m、质量为m1=0.5kg的木板A,一质量为m2=1kg的小物体B以初速度υ0=4m/s滑上A的上表面,A与B之间的动摩擦因数为μ=0.2,g=10m/s2;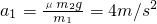
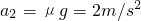
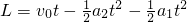 代入数值解得:t=1s或
代入数值解得:t=1s或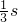 .
.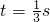
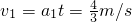
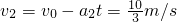
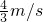 、
、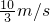 .
.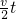 ①
①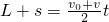 ②
②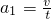 ③
③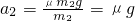 ④
④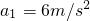


科目:高中物理 来源: 题型:
 如图所示,在足够长的粗糙水平桌面上,静止放置质量为m1=0.20
如图所示,在足够长的粗糙水平桌面上,静止放置质量为m1=0.20查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,在足够长的光滑水平轨道上静止三个小木块A、B、C,质量分别为mA=1kg,mB=1kg,mC=2kg,其中B与C用一个轻弹簧固定连接,开始时整个装置处于静止状态;A和B之间有少许塑胶炸药,A的左边有一个弹性挡板(小木块和弹性挡板碰撞过程没有能量损失).现在引爆塑胶炸药,若炸药爆炸产生的能量有E=9J转化为A和B沿轨道方向的动能,A和B分开后,A恰好在B、C之间的弹簧第一次恢复到原长时追上B,并且与B发生碰撞后粘在一起.求:
如图所示,在足够长的光滑水平轨道上静止三个小木块A、B、C,质量分别为mA=1kg,mB=1kg,mC=2kg,其中B与C用一个轻弹簧固定连接,开始时整个装置处于静止状态;A和B之间有少许塑胶炸药,A的左边有一个弹性挡板(小木块和弹性挡板碰撞过程没有能量损失).现在引爆塑胶炸药,若炸药爆炸产生的能量有E=9J转化为A和B沿轨道方向的动能,A和B分开后,A恰好在B、C之间的弹簧第一次恢复到原长时追上B,并且与B发生碰撞后粘在一起.求:查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,在足够长的光滑绝缘水平直线轨道上方h高度的P点,固定一电荷量为+Q的点电荷.一质量为m、带电荷量为+q的物块(可视为质点),从轨道上的A点以初速度v0沿轨道向右运动,当运动到P点正下方B点时速度为v.已知点电荷产生的电场在A点的电势为φ(取无穷远处电势为零),PA连线与水平轨道的夹角为60°,试求:
如图所示,在足够长的光滑绝缘水平直线轨道上方h高度的P点,固定一电荷量为+Q的点电荷.一质量为m、带电荷量为+q的物块(可视为质点),从轨道上的A点以初速度v0沿轨道向右运动,当运动到P点正下方B点时速度为v.已知点电荷产生的电场在A点的电势为φ(取无穷远处电势为零),PA连线与水平轨道的夹角为60°,试求:查看答案和解析>>
科目:高中物理 来源: 题型:
 (2011?海淀区模拟)如图所示,在足够长的光滑水平轨道上有三个小木块A、B、C,质量分别为mA、mB、mC,且mA=mB=1.0kg,mC=2.0kg,其中B与C用一个轻弹簧拴接在一起,开始时整个装置处于静止状态.A和B之间有少许塑胶炸药,A的左边有一个弹性挡板.现在引爆塑胶炸药,若炸药爆炸产生的能量中有E=9.0J转化为A和B的动能,A和B分开后,A恰好在B、C之间的弹簧第一次恢复到原长时追上B,并且与B发生碰撞后粘在一起.忽略小木块和弹性挡板碰撞过程中的能量损失.求:
(2011?海淀区模拟)如图所示,在足够长的光滑水平轨道上有三个小木块A、B、C,质量分别为mA、mB、mC,且mA=mB=1.0kg,mC=2.0kg,其中B与C用一个轻弹簧拴接在一起,开始时整个装置处于静止状态.A和B之间有少许塑胶炸药,A的左边有一个弹性挡板.现在引爆塑胶炸药,若炸药爆炸产生的能量中有E=9.0J转化为A和B的动能,A和B分开后,A恰好在B、C之间的弹簧第一次恢复到原长时追上B,并且与B发生碰撞后粘在一起.忽略小木块和弹性挡板碰撞过程中的能量损失.求:查看答案和解析>>
科目:高中物理 来源: 题型:
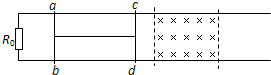 如图所示,在足够长的两条平行金属导轨的左端接有一个定值电阻R0,两导轨间的距离L=0.5m,在虚线的区域内有与导轨平面垂直的匀强磁场,磁感应强度B=0.2T,虚线间的距离S=1.0m.完全相同的金属棒ab、cd与导轨垂直放置,两棒间用2.0m长的绝缘轻杆连接.棒与导轨间无摩擦,两棒电阻皆为r=0.3Ω,导轨电阻不计.已知R0=2r.现用一外力从图示位置水平向右拉cd棒,使两棒以v=5.0m/s的速度向右匀速穿过磁场区域.求:
如图所示,在足够长的两条平行金属导轨的左端接有一个定值电阻R0,两导轨间的距离L=0.5m,在虚线的区域内有与导轨平面垂直的匀强磁场,磁感应强度B=0.2T,虚线间的距离S=1.0m.完全相同的金属棒ab、cd与导轨垂直放置,两棒间用2.0m长的绝缘轻杆连接.棒与导轨间无摩擦,两棒电阻皆为r=0.3Ω,导轨电阻不计.已知R0=2r.现用一外力从图示位置水平向右拉cd棒,使两棒以v=5.0m/s的速度向右匀速穿过磁场区域.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com