
| A. | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{(R+{h}_{1})^{2}}{(R+{h}_{2})^{2}}$,$\frac{{T}_{1}}{{T}_{2}}$=($\frac{R+{h}_{1}}{R+{h}_{2}}$)${\;}^{\frac{3}{2}}$ | |
| B. | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{(R+{h}_{2})^{2}}{(R+{h}_{1})^{2}}$,$\frac{{T}_{1}}{{T}_{2}}$=($\frac{R+{h}_{1}}{R+{h}_{2}}$)${\;}^{\frac{3}{2}}$ | |
| C. | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{(R+{h}_{1})^{2}}{(R+{h}_{2})^{2}}$,$\frac{{T}_{1}}{{T}_{2}}$=($\frac{R+{h}_{1}}{R+{h}_{2}}$)${\;}^{\frac{2}{3}}$ | |
| D. | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{(R+{h}_{2})^{2}}{(R+{h}_{1})^{2}}$,$\frac{{T}_{1}}{{T}_{2}}$=($\frac{R+{h}_{2}}{R+{h}_{1}}$)${\;}^{\frac{2}{3}}$ |
分析 嫦娥号绕月球圆周运动万有引力提供圆周运动向心力,据此根据半径关系求解向心加速度与周期之比.
解答 解:根据万有引力提供圆周运动向心力有:$G\frac{mM}{{r}^{2}}=ma=mr\frac{4{π}^{2}}{{T}^{2}}$
可得:$a=\frac{GM}{{r}^{2}}$即:$\frac{{a}_{1}}{{a}_{2}}=(\frac{{r}_{2}}{{r}_{1}})^{2}=(\frac{R+{h}_{2}}{R+{h}_{1}})^{2}$
周期为:;T=$\sqrt{\frac{4{π}^{2}{r}^{3}}{GM}}$
可得:$\frac{{T}_{1}}{{T}_{2}}=\sqrt{(\frac{{r}_{1}}{{r}_{2}})^{3}}=(\frac{R+{h}_{1}}{R+{h}_{2}})^{\frac{3}{2}}$
所以B正确,ACD错误.
故选:B.
点评 万有引力提供圆周运动向心力是解决本题的关键,求得向心加速度和周期的表达式,再根据半径关系分析求解即可.


科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
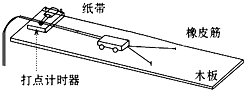 探究力对原来静止的物体做的功与物体获得的速度的关系时,实验装置如图所示,实验主要过程如下:
探究力对原来静止的物体做的功与物体获得的速度的关系时,实验装置如图所示,实验主要过程如下:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
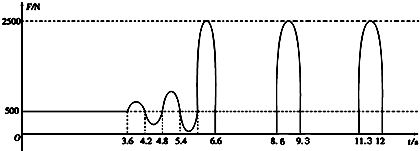
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
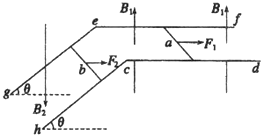 如图所示,足够长的光滑平行金属导轨cd和ef水平放置,在其左端连接倾角为θ=37°的光滑金属导轨ge,hc,导轨间距均为L=1m,在水平导轨和倾斜导轨上,各放一根与导轨垂直的金属杆,金属杆与导轨接触良好.金属杆a,b质量均为m=0.1kg,电阻Ra=2Ω、Rb=3Ω,其余电阻不计.在水平导轨和斜面导轨区域分别有竖直向上和竖直向下的匀强磁场B1、B2,且B1=B2=0.5T.已知从t=0时刻起,杆a在水平外力F1作用下由静止开始向右做直线运动,杆b在水平向右的外力F2作用下始终保持静止状态,且F2=0.75+0.2t(N).(sin37°=0.6,cos37°=0.8取10m/s2).求:
如图所示,足够长的光滑平行金属导轨cd和ef水平放置,在其左端连接倾角为θ=37°的光滑金属导轨ge,hc,导轨间距均为L=1m,在水平导轨和倾斜导轨上,各放一根与导轨垂直的金属杆,金属杆与导轨接触良好.金属杆a,b质量均为m=0.1kg,电阻Ra=2Ω、Rb=3Ω,其余电阻不计.在水平导轨和斜面导轨区域分别有竖直向上和竖直向下的匀强磁场B1、B2,且B1=B2=0.5T.已知从t=0时刻起,杆a在水平外力F1作用下由静止开始向右做直线运动,杆b在水平向右的外力F2作用下始终保持静止状态,且F2=0.75+0.2t(N).(sin37°=0.6,cos37°=0.8取10m/s2).求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
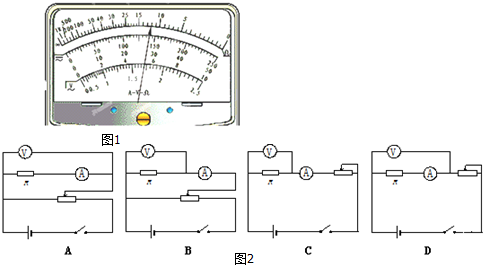
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
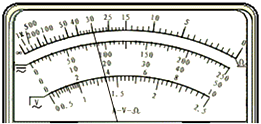 (1)用多用表的欧姆档测量阻值约为几十kΩ的电阻Rx,以下给出的是可能的操作步骤,其中S为选择开关,P为欧姆档调零旋钮,把你认为正确的步骤前的字母按合理的顺序填写在下面的横线上.
(1)用多用表的欧姆档测量阻值约为几十kΩ的电阻Rx,以下给出的是可能的操作步骤,其中S为选择开关,P为欧姆档调零旋钮,把你认为正确的步骤前的字母按合理的顺序填写在下面的横线上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com