
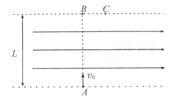
 ��ͼ��ʾ���ڿ���ΪL����������������ǿ�糡���糡�ķ���ƽ��������߽磬һ���������Ӵ��±߽��ϵ�A�㣬�Գ��ٶ�v0�ش�ֱ�ڵ糡��AB��������糡�����ϱ߽��C���������֪���ӵ��������ƣ��ϱ߽���BC�����Ϊ$\frac{1}{4}$L��
��ͼ��ʾ���ڿ���ΪL����������������ǿ�糡���糡�ķ���ƽ��������߽磬һ���������Ӵ��±߽��ϵ�A�㣬�Գ��ٶ�v0�ش�ֱ�ڵ糡��AB��������糡�����ϱ߽��C���������֪���ӵ��������ƣ��ϱ߽���BC�����Ϊ$\frac{1}{4}$L������ ��1�����������ڵ糡��������ƽ���˶���ˮƽ���˶����ȼ���ֱ���˶�����ֱ���˶�������ֱ���˶������ݷ��˶���ʽ��ʽ��⣻
��2�����ݷ��˶���ʽ���õ����ٶȵı���ʽ���з������ɣ�
��� �⣺��1������������ƽ���˶�����ˮƽ����Ϊx�ᣬ��ֱ����Ϊy�ᣬ���˶����������ֽ⣬ˮƽ���˶���$\frac{L}{4}={\frac{{v}_{x}}{2}}_{\;}t$��
��ֱ���˶���L=v0t��
������ã�${v}_{x}=\frac{{v}_{0}}{2}$��
�ʺ��ٶȴ�С��v=$\sqrt{{v}_{x}^{2}+{v}_{0}^{2}}=\frac{\sqrt{5}}{2}{v}_{0}$��
���ٶȷ�������ֱ����ļнǵ�����ֵ��tan��=$\frac{{v}_{x}}{{v}_{0}}=\frac{1}{2}$��
��2������һ���У���ˮƽ���˶����У�${v}_{x}=at=\frac{qE}{m}•\frac{L}{{v}_{0}}=\frac{{v}_{0}}{2}$����E=$\frac{m{v}_{0}^{2}}{2qL}$��
����������ƽ���˶�����ֱ���˶���L=v1t��
ˮƽ���˶���vx=at=$\frac{qE}{m}t$��
��${v}_{x}=\frac{{v}_{0}^{2}}{2{v}_{1}}$��
���ٶȴ�С��v=$\sqrt{{v}_{x}^{2}+{v}_{1}^{2}}$=$\sqrt{\frac{{v}_{0}^{4}}{4{v}_{1}^{2}}+{v}_{1}^{2}}$��
��ϱ���ʽ֪ʶ���У�$\frac{v_0^4}{4v_1^2}+v_1^2��2\sqrt{\frac{v_0^4}{4v_1^2}}•\sqrt{v_1^2}=v_0^2$����$\frac{v_0^4}{4v_1^2}=v_1^2$����${v}_{1}=\frac{{v}_{0}}{2}$ʱȡ�Ⱥţ���
�ʵ����ٶ�${v}_{1}=\frac{{v}_{0}}{2}$ʱ�����ٶȴ�С����СֵΪv0��
�𣺣�1�����Ӿ���C��ʱ���ٶȴ�СΪ$\frac{\sqrt{5}}{2}{v}_{0}$���ٶȷ�������ֱ����ļнǵ�����ֵΪ$\frac{1}{2}$��
��2�����������ӵ������ٶȴ�С����Ϊ����ֵ��ԶС�ڹ��٣����������Ӵ��ϱ߽����ʱ�ٶȵ���СֵΪv0��
���� ���⿼��������ƫת�糡�е��˶���Ҫ���������ֽⷨ����Ϸ��˶���ʽ��ʽ�������ڶ���Ҫ�����ѧ����ʽ���з�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
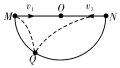 ͬʱ������С����v1��v2���ٶ�����ͼ��ʾ�ķ����׳�����������պ�����һ������Ϊ��Բ�εĿ���ͬһ��Q����֪��MOQ=60�㣮���Կ�����������������˵����ȷ���ǣ�������
ͬʱ������С����v1��v2���ٶ�����ͼ��ʾ�ķ����׳�����������պ�����һ������Ϊ��Բ�εĿ���ͬһ��Q����֪��MOQ=60�㣮���Կ�����������������˵����ȷ���ǣ�������| A�� | $\frac{{v}_{1}}{{v}_{2}}$=$\frac{1}{3}$ | |
| B�� | ������v1��v2���������ڿ���������Q���Ҳ� | |
| C�� | ����ij��ٶ����������仯��ֻҪ���ڿ��е�ͬһ�㣬v1+v2��Ϊ���� | |
| D�� | ��������v1��������������ڿ���ǰ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
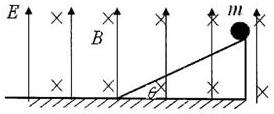
 ��ͼ��ʾ��һ���Ϊ�ȵĹ⻬б��̶���ˮƽ���ϣ�б���㹻����һ����Ϊm�Ĵ�����������б�����ϵ���ǿ�糡E�����£���б����ɾ�ֹ��б���������ȼ���ֱ���˶�����ʱ��t�������ܼ�����120J����ʱ��ȥ�糡��֮�������־�����ͬ��ʱ��t�ص�б��ˣ����Ե���Ϊ�����������棬��֪�������ٶ�Ϊg��������˵����ȷ���ǣ�������
��ͼ��ʾ��һ���Ϊ�ȵĹ⻬б��̶���ˮƽ���ϣ�б���㹻����һ����Ϊm�Ĵ�����������б�����ϵ���ǿ�糡E�����£���б����ɾ�ֹ��б���������ȼ���ֱ���˶�����ʱ��t�������ܼ�����120J����ʱ��ȥ�糡��֮�������־�����ͬ��ʱ��t�ص�б��ˣ����Ե���Ϊ�����������棬��֪�������ٶ�Ϊg��������˵����ȷ���ǣ�������| A�� | ����ص�б��˵Ķ���Ϊ60J | |
| B�� | ����������Ϊq=$\frac{2mgsin��}{E}$ | |
| C�� | ��ȥ�糡ʱ�����������������90J | |
| D�� | ��ǰһ��ʱ��t��һ��������ֶ���������������ȵ�ʱ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
 ��ͼ��ʾ���ռ��ڴ��ڴ�ֱֽ���������ǿ�ų�����ֱ���ϵ���ǿ�糡��һ����С����Ϊ�ʵ㣩����m=0.4kg�������q=-0.8C������Ǧ�=37��Ĺ⻬б����ߵ��ɾ�ֹ��ʼ�»�������б���»�����s=$\frac{8}{3}$mʱ��б�����룮��ʱ�������糡����С��������Բ���˶�������ǡ�ò�����淢����ײ���������ٶ�g=10m/s2����
��ͼ��ʾ���ռ��ڴ��ڴ�ֱֽ���������ǿ�ų�����ֱ���ϵ���ǿ�糡��һ����С����Ϊ�ʵ㣩����m=0.4kg�������q=-0.8C������Ǧ�=37��Ĺ⻬б����ߵ��ɾ�ֹ��ʼ�»�������б���»�����s=$\frac{8}{3}$mʱ��б�����룮��ʱ�������糡����С��������Բ���˶�������ǡ�ò�����淢����ײ���������ٶ�g=10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
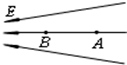 ��ͼ�ǵ糡��ij����ĵ糡�߷ֲ�ͼ��A��B�ǵ糡�е����㣬�����жϸõ糡�ķ���������ѡ��������ҡ����������ж�A�㳡ǿ��С��ѡ�A����B������һ��������B���ܵ��糡���ķ���������ѡ��� �����ҡ�����
��ͼ�ǵ糡��ij����ĵ糡�߷ֲ�ͼ��A��B�ǵ糡�е����㣬�����жϸõ糡�ķ���������ѡ��������ҡ����������ж�A�㳡ǿ��С��ѡ�A����B������һ��������B���ܵ��糡���ķ���������ѡ��� �����ҡ������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
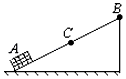 ��ͼ��ʾ�����壨�ɿ����ʵ㣩��4m/s�ij��ٶ���б���A�㻬�Ϲ⻬б�����ȼ���ֱ���˶���;��б���е�C��������ߵ�B����֪��A��C���ٶ�vA��vC=4��3����C�㵽B����ʱ��3-$\sqrt{2}$��s������
��ͼ��ʾ�����壨�ɿ����ʵ㣩��4m/s�ij��ٶ���б���A�㻬�Ϲ⻬б�����ȼ���ֱ���˶���;��б���е�C��������ߵ�B����֪��A��C���ٶ�vA��vC=4��3����C�㵽B����ʱ��3-$\sqrt{2}$��s�������鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com