
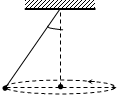
 如图所示的圆锥摆,摆线与竖线的夹角为θ,则小球的向心加速度为gtanθ;若摆球的质量为m,则向心力的大小等于mgtanθ,绳子的受到的拉力为$\frac{mg}{cosθ}$.
如图所示的圆锥摆,摆线与竖线的夹角为θ,则小球的向心加速度为gtanθ;若摆球的质量为m,则向心力的大小等于mgtanθ,绳子的受到的拉力为$\frac{mg}{cosθ}$. 分析 对小球进行受力分析,找出向心力,结合几何关系和牛顿运动定律求解.
解答 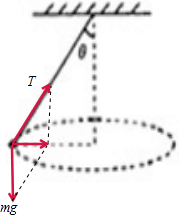 解:小球只受重力和绳子的拉力两个力的作用,如图所示,向心力是重力和绳子的拉力的合力,根据牛顿第二定律得:
解:小球只受重力和绳子的拉力两个力的作用,如图所示,向心力是重力和绳子的拉力的合力,根据牛顿第二定律得:
小球的向心力为:F=mgtanθ,则向心加速度为:a=$\frac{F}{m}$=gtanθ.
绳子的受到的拉力为 T=$\frac{mg}{cosθ}$
故答案为:gtanθ,mgtanθ,$\frac{mg}{cosθ}$.
点评 解答该题首先要求要会正确的受力分析,在对物体进行受力分析时,像向心力及下滑力之类的力是不能分析的.要严格按照受力分析的一般步骤,不能漏掉力,也不能添加力.同时要会熟练的对力进行正确的合成和分解.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中物理 来源: 题型:填空题
 如图所示,在倾角为θ的光滑斜面上有一长为l的细线,细线一端固定在0点,另一端拴一质量为m的小球,现使小球恰好能在斜面上做完整的圆周运动.已知O点到斜面底边的距离SOC=L,则小球通过最高点A时的速度vA=$\sqrt{glsinθ}$;小球通过最低点B时细线对小球的拉力T=6mgsinθ.
如图所示,在倾角为θ的光滑斜面上有一长为l的细线,细线一端固定在0点,另一端拴一质量为m的小球,现使小球恰好能在斜面上做完整的圆周运动.已知O点到斜面底边的距离SOC=L,则小球通过最高点A时的速度vA=$\sqrt{glsinθ}$;小球通过最低点B时细线对小球的拉力T=6mgsinθ.查看答案和解析>>
科目:高中物理 来源: 题型:填空题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
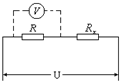 如图所示,R为定值电阻,Rx为侍测电阻,电压U为一定值.用一只伏特表分别测量R和Rx上的电压,示数分别为U1和U2,发现U1+U2<U.则关于Rx阻值的下列说法中,正确的是( )
如图所示,R为定值电阻,Rx为侍测电阻,电压U为一定值.用一只伏特表分别测量R和Rx上的电压,示数分别为U1和U2,发现U1+U2<U.则关于Rx阻值的下列说法中,正确的是( )| A. | 精确等于$\frac{U_2}{U_1}R$ | |
| B. | 近似等于$\frac{U_2}{U_1}R$ | |
| C. | 当伏特表内阻RV比R、Rx都大的多时才近似等于$\frac{U_2}{U_1}R$ | |
| D. | 因伏特表的内阻未知,上述说法都不正确 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
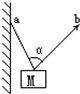 用两根细线a和b悬挂一个物体M,使之静止,a和b的夹角α=60°,如图所示,缓慢移动b线上端的施力点最后使b水平,在这一过程中M的位置一直不变.则在b线移动过程中a线与b线拉力大小变化情况是( )
用两根细线a和b悬挂一个物体M,使之静止,a和b的夹角α=60°,如图所示,缓慢移动b线上端的施力点最后使b水平,在这一过程中M的位置一直不变.则在b线移动过程中a线与b线拉力大小变化情况是( )| A. | a线上拉力不断增大 | B. | b线上拉力不断增大 | ||
| C. | b线上拉力先减小后增大 | D. | a线上拉力保持不变 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,一木块放在水平面上,在水平方向上施加外力F1=10N,F2=2N,木块处于静止状态.若撤去外力F1,则木块受到的摩擦力大小为2N,方向水平向右.
如图所示,一木块放在水平面上,在水平方向上施加外力F1=10N,F2=2N,木块处于静止状态.若撤去外力F1,则木块受到的摩擦力大小为2N,方向水平向右.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 小车、木块、摆球的速度都发生变化,分别变为 v1、v2、v3,满足 (M+m0)V=Mv1+mv2+m0v3 | |
| B. | 摆球的速度不变,小车和木块的速度变为 v1和 v2,满足 MV═Mv1+mv2 | |
| C. | 摆球的速度不变,小车和木块的速度都变为v,满足(M+m0)V=(M+m)v | |
| D. | 小车和摆球的速度都变为v1,木块的速度变为v2,满足 (M+m0)V=(M+m0)v1+mv2 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
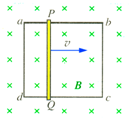 如图所示,固定在匀强磁场中的正方形导线框abcd边长为L,其中ab边是电阻为R的均匀电阻丝,其余三边是电阻可忽略的铜导线.匀强磁场的磁感应强度为B,方向垂直于纸面向里,现有一段长短、粗细、材料均与ab边相同的电阻丝PQ架在线框上,并以恒定速度v从ad边滑向bc边,PQ在滑动过程中与导线框的接触良好.当PQ滑过$\frac{L}{3}$的距离时,通过aP段电阻丝的电流是多大?方向如何?
如图所示,固定在匀强磁场中的正方形导线框abcd边长为L,其中ab边是电阻为R的均匀电阻丝,其余三边是电阻可忽略的铜导线.匀强磁场的磁感应强度为B,方向垂直于纸面向里,现有一段长短、粗细、材料均与ab边相同的电阻丝PQ架在线框上,并以恒定速度v从ad边滑向bc边,PQ在滑动过程中与导线框的接触良好.当PQ滑过$\frac{L}{3}$的距离时,通过aP段电阻丝的电流是多大?方向如何?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com