
 如图所示,内壁光滑的木槽质量mA=0.1kg,内径为2m,置于水平桌面上,槽与桌面间的动摩擦因数为μ=0.3.槽内有两个可视为质点的小球B和C,它们的质量分别是mB=0.1kg、mC=0.2kg.现用两球将很短的轻弹簧压紧(球与弹簧不连接),且B球到木槽左端、C球到木槽右端的距离均为L=1m,这时弹簧的弹性势能为Ep=0.3J.同时释放B、C球,并假设小球与槽碰撞后不分离,碰撞时间极短,g=10m/s2,求:
如图所示,内壁光滑的木槽质量mA=0.1kg,内径为2m,置于水平桌面上,槽与桌面间的动摩擦因数为μ=0.3.槽内有两个可视为质点的小球B和C,它们的质量分别是mB=0.1kg、mC=0.2kg.现用两球将很短的轻弹簧压紧(球与弹簧不连接),且B球到木槽左端、C球到木槽右端的距离均为L=1m,这时弹簧的弹性势能为Ep=0.3J.同时释放B、C球,并假设小球与槽碰撞后不分离,碰撞时间极短,g=10m/s2,求:分析 (1)分别对BC和AB为研究对象,由动量守恒及机械能守恒可求得第1个小球一槽碰撞后的共同速度;
(2)AB相撞后,一起向左做匀减速运动,由牛顿第二定律可求得共同的加速度;由运动学公式可求得运动时间,则可判断C与相撞是A是否停止,再由动量守恒可求得共同速度;
(3)物体之间的相互摩擦产生热量,由功能关系即可求出产生的总热量.
解答 解:(1、2)释放瞬间,系统动量守恒,根据动量守恒定律得:mBvB=mCvC…①
根据机械能守恒定律得:${E_P}=\frac{1}{2}{m_B}{v_B}^2+\frac{1}{2}{m_C}{v_C}^2$…②
联立①②得:vB=2m/s,vC=1m/s
第一个小球与槽碰撞过程中,系统动量守恒,以B球速度方向为正方向,根据动量守恒定律得:mBvB=(mB+mA)v1…③
代入数据得:v1=1m/s,方向水平向左
对AB整体有:μ(mB+mA+mC)g=(mB+mA)a
代入数据得:a=6m/s2
AB整体开始运动到速度减为0的时间为:$t=\frac{v_1}{a}=\frac{1}{6}s$
经过的位移为:${s_1}=\frac{{0+{v_1}}}{2}t=\frac{0+1}{2}×\frac{1}{6}=\frac{1}{12}m$
在这段时间里,C走过的位移为:${s_C}={v_C}t=\frac{1}{6}m$
因为${s_1}+{s_C}<\frac{L}{2}$,故AB是停下来后与C发生碰撞.
mCvC=(mB+mA+mC)v2
代入数据得:v2=0.5m/s,方向水平向右
(3)槽与桌面间因摩擦而产生的热量为:
$\begin{array}{l}Q={Q_1}+{Q_2}=μ({m_B}+{m_A}+m{\;}_C)g{s_1}+\frac{1}{2}({m_B}+{m_A}+m{\;}_C){v_2}^2\\=0.1+0.05=0.15J\\.\end{array}$
答:(1)第一个小球与槽碰撞后的共同速度大小为1m/s,方向水平向左.
(2)第二个小球与槽碰撞后的共同速度大小为0.5m/s,方向水平向右.
(3)整个运动过程中,槽与桌面间因摩擦而产生的热量为0.15J
点评 木题考查动量守恒定律及功能关系的综合应用,在解题时要注意各过程中守恒的量,从而得出守恒关系进行解题.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:填空题
 估计你正常情况下的心跳周期是0.8 秒,假如这是你心电图的一部分,若每小格的宽度是0.5cm,则测量心电图时记录纸被拖动的速率是1.875cm/s.
估计你正常情况下的心跳周期是0.8 秒,假如这是你心电图的一部分,若每小格的宽度是0.5cm,则测量心电图时记录纸被拖动的速率是1.875cm/s.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,匀强电场方向与匀强磁场方向互相垂直,已知磁感应强度为0.1T,两板间的距离为2cm,若速度为3×105m/s的电子穿过正交的电场和磁场时,不改变方向,则( )
如图所示,匀强电场方向与匀强磁场方向互相垂直,已知磁感应强度为0.1T,两板间的距离为2cm,若速度为3×105m/s的电子穿过正交的电场和磁场时,不改变方向,则( )| A. | 上板带正电 | B. | 下板带正电 | ||
| C. | 两板间的电压6×103V | D. | 两板间的电压1.5×103V |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,有一个劲度系数为200N/m的绝缘弹簧,在其下端放一个带电量大小为q=2C、质量为m=1kg的小球,若在空间当中加一个竖直向上的匀强电场,弹簧总共伸长了10cm.求:
如图所示,有一个劲度系数为200N/m的绝缘弹簧,在其下端放一个带电量大小为q=2C、质量为m=1kg的小球,若在空间当中加一个竖直向上的匀强电场,弹簧总共伸长了10cm.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
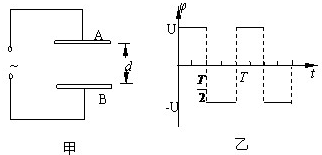
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 一束电子流在经U=1000V的加速场A加速后,在距两极板等距处垂直进入B平行板间的匀强电场,如图所示,已知电子质量为m=9×10-31kg,若两板间d=4.0cm,板长l=20.0cm,那么B板间加多少的电压,电子刚好从下板飞出.
一束电子流在经U=1000V的加速场A加速后,在距两极板等距处垂直进入B平行板间的匀强电场,如图所示,已知电子质量为m=9×10-31kg,若两板间d=4.0cm,板长l=20.0cm,那么B板间加多少的电压,电子刚好从下板飞出.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 现用伏安法研究某电子器件R1(6V,2.5W)的伏安特性曲线,要求特性曲线尽可能完整(直接测量的变化范围尽可能大一些),备有下列器材:
现用伏安法研究某电子器件R1(6V,2.5W)的伏安特性曲线,要求特性曲线尽可能完整(直接测量的变化范围尽可能大一些),备有下列器材: ”表示).
”表示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com