
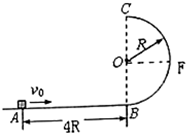
 如图所示,水平不光滑轨道AB与半圆形光滑的竖直圆轨道BC相连,B点与C点的连线沿竖直方向,AB段长为4R,圆轨道的半径为R.一个小滑块以初速度$\sqrt{8gR}$从A点开始沿轨道滑动,已知它运动到C点时对轨道的压力大小恰好等于其重力,已知小球质量为m.重力加速度为g.求:
如图所示,水平不光滑轨道AB与半圆形光滑的竖直圆轨道BC相连,B点与C点的连线沿竖直方向,AB段长为4R,圆轨道的半径为R.一个小滑块以初速度$\sqrt{8gR}$从A点开始沿轨道滑动,已知它运动到C点时对轨道的压力大小恰好等于其重力,已知小球质量为m.重力加速度为g.求:分析 (1)先由牛顿第二定律可求得C点的速度,从A到C,运用动能定理列式可解得滑块与水平轨道间的动摩擦因数.
(2)从F到C的过程,由动能定理求出F点的速度,再由牛顿第二定律求解轨道对小球的作用力,即可得到小球对轨道的作用力.
(3)小球离开C点后作平抛运动,由分位移公式求出C点的速度,再由动能定理求解v0.
解答 解:(1)据题在C点有:mg+mg=m$\frac{{v}_{c}^{2}}{R}$,
得:vC=$\sqrt{2gR}$
从A到C的过程中,由动能定理得:
-μmg•4R-mg•2R=$\frac{1}{2}m{v}_{C}^{2}$-$\frac{1}{2}m{v}_{A}^{2}$
又 vA=$\sqrt{8gR}$
联立以上三式得:μ=0.25
(2)从F到C的过程,由动能定理得:
-mgR=$\frac{1}{2}m{v}_{C}^{2}$-$\frac{1}{2}m{v}_{F}^{2}$
在F点,由牛顿第二定律得:F′=m$\frac{{v}_{F}^{2}}{R}$
可得:F′=4mg
由牛顿第三定律得:F=F′=4mg
(3)小球离开C点后作平抛运动,则得:
2R=$\frac{1}{2}g{t}^{2}$
4R=vCt
联立可得:vC=2$\sqrt{gR}$
根据动能定理得:
-μmg•4R-mg•2R=$\frac{1}{2}m{v}_{C}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$
解得:v0=2$\sqrt{3gR}$
答:(1)滑块与水平轨道间的动摩擦因数是0.25;
(2)圆周BC上有一个和圆心O点等高的F点,当小球到达F点时小球对轨道的作用力是4mg.
(3)假设改变v0的大小,使得小球到达C点后离开轨道作平抛运动,恰好到达A点,此时v0为2$\sqrt{3gR}$.
点评 对于多过程的题目,一定要明确物体的运动过程,通过分析从而找出正确的解题方法.一般来说涉及力在空间的效果优先考虑动能定理.


科目:高中物理 来源: 题型:选择题
 如图所示,是美国的“卡西尼”号探测器经过长达7年的“艰苦”旅行,进入绕土星飞行的轨道.若“卡西尼”号探测器在半径为R的土星上空离土星表面高h的圆形轨道上绕土星飞行,环绕n周飞行时间为t,已知引力常量为G,则下列关于土星质量M和平均密度ρ的表达式正确的是( )
如图所示,是美国的“卡西尼”号探测器经过长达7年的“艰苦”旅行,进入绕土星飞行的轨道.若“卡西尼”号探测器在半径为R的土星上空离土星表面高h的圆形轨道上绕土星飞行,环绕n周飞行时间为t,已知引力常量为G,则下列关于土星质量M和平均密度ρ的表达式正确的是( )| A. | M=$\frac{4{π}^{2}(R+h)^{3}}{G{t}^{2}}$,ρ=$\frac{3π(R+h)^{3}}{G{t}^{2}{R}^{3}}$ | |
| B. | M=$\frac{4{π}^{2}{n}^{2}(R+h)^{2}}{G{t}^{2}}$,ρ=$\frac{3π{n}^{2}(R+h)^{2}}{G{t}^{2}{R}^{3}}$ | |
| C. | M=$\frac{4{π}^{2}{t}^{2}(R+h)^{3}}{G{n}^{2}}$,ρ=$\frac{3π{t}^{2}(R+h)^{3}}{G{n}^{2}{R}^{3}}$ | |
| D. | M=$\frac{4{π}^{2}{n}^{2}(R+h)^{3}}{G{t}^{2}}$,ρ=$\frac{3π{n}^{2}(R+h)^{3}}{G{t}^{2}{R}^{3}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 在医院里常用如图所示装置对小腿受伤的病人进行牵引治疗.不计滑轮组的摩擦和绳子的质量,绳子下端所挂重物的质量是5kg.问:病人的腿所受水平方向的牵引力是多大?(g=10m/s2)
在医院里常用如图所示装置对小腿受伤的病人进行牵引治疗.不计滑轮组的摩擦和绳子的质量,绳子下端所挂重物的质量是5kg.问:病人的腿所受水平方向的牵引力是多大?(g=10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{Mh}{M+m}$ | B. | $\frac{mh}{M+m}$ | C. | $\frac{(m+M)h}{M}$ | D. | $\frac{(m+M)h}{m}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 满足能量守恒定律的宏观过程都是可以自发进行的 | |
| B. | 所有的晶体都有固定的熔点 | |
| C. | 气体对外做功,其内能可能增加 | |
| D. | 当分子间距离增大时,分子间引力增大,而分子间斥力减小 | |
| E. | 水可以浸润玻璃,但是不能浸润石蜡,这个现象表明一种液体是否浸润某种固体与这两种物质的性质都有关系 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 波长可能是12m | B. | 波长一定是4m | C. | 周期一定是2s | D. | 波速可能是10m/s |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,一电子在外力作用下沿等量异种电荷的中垂线由A→O→B匀速运动,A、B两点关于两电荷连线对称,电子重力不计,则电子运动过程中说法正确的是( )
如图所示,一电子在外力作用下沿等量异种电荷的中垂线由A→O→B匀速运动,A、B两点关于两电荷连线对称,电子重力不计,则电子运动过程中说法正确的是( )| A. | 电子受外力先变大后变小,方向水平向右 | |
| B. | 电子受外力先变小后变大,方向水平向左 | |
| C. | 电子在A、B两点电势能相等 | |
| D. | 电子受合力为零 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 伽利略最早指出力是维持物体运动的原因 | |
| B. | 开普勒利用自己长期观测的数据发现了行星运动的规律 | |
| C. | 牛顿利用自己发现的万有引力定律首次测出了地球的质量 | |
| D. | 笛卡尔对牛顿第一定律的建立做出了贡献 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com