
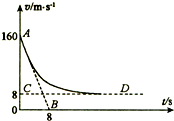
 “神舟七号”飞船完成了预定空间科学和技术实验任务后,返回舱于2008年9月28日17时37分开始从太空向地球表面按预定轨道返回,在离地10km 的高度打开阻力降落伞减速下降,这一过程中若返回舱所受阻力与速度的平方成正比,比例系数(空气阻力系数)为k.设返回舱总质量M=3000kg,所受空气浮力恒定不变,且认为竖直降落.从某时刻开始计时.返回舱的运动v--t图象如图中的AD曲线所示,图中AB是曲线在A点的切线,切线交于横轴一点B的坐标为(8,0),CD是平行横轴的直线,交纵轴于C点,c的坐标为(0,8).g取10m/s2,请回答下列问题:
“神舟七号”飞船完成了预定空间科学和技术实验任务后,返回舱于2008年9月28日17时37分开始从太空向地球表面按预定轨道返回,在离地10km 的高度打开阻力降落伞减速下降,这一过程中若返回舱所受阻力与速度的平方成正比,比例系数(空气阻力系数)为k.设返回舱总质量M=3000kg,所受空气浮力恒定不变,且认为竖直降落.从某时刻开始计时.返回舱的运动v--t图象如图中的AD曲线所示,图中AB是曲线在A点的切线,切线交于横轴一点B的坐标为(8,0),CD是平行横轴的直线,交纵轴于C点,c的坐标为(0,8).g取10m/s2,请回答下列问题: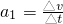 =
=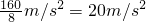
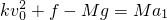

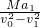

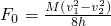
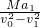 ,数值k=2.35kg/m
,数值k=2.35kg/m

科目:高中物理 来源: 题型:
 2008年9月25日21时10分,神舟七号飞船成功发射,共飞行2天20小时27分钟,绕地球飞行45圈后,于9月28日17时37分安全着陆.航天员翟志刚着“飞天”舱外航天服,在刘伯明的配合下,成功完成了空间出舱活动,进行了太空行走.出舱活动结束后,释放了伴飞卫星,并围绕轨道舱进行伴飞实验.神舟七号是由长征-2F运载火箭将其送入近地点为A,远地点为B的椭圆轨道上,实施变轨后,进入预定圆轨道,其简化的模拟轨道如图12所示.假设近地点A距地面高度为h,飞船在预定圆轨道上飞行n圈所用的时间为t,地球表面的重力加速度为g,地球半径R,试求:
2008年9月25日21时10分,神舟七号飞船成功发射,共飞行2天20小时27分钟,绕地球飞行45圈后,于9月28日17时37分安全着陆.航天员翟志刚着“飞天”舱外航天服,在刘伯明的配合下,成功完成了空间出舱活动,进行了太空行走.出舱活动结束后,释放了伴飞卫星,并围绕轨道舱进行伴飞实验.神舟七号是由长征-2F运载火箭将其送入近地点为A,远地点为B的椭圆轨道上,实施变轨后,进入预定圆轨道,其简化的模拟轨道如图12所示.假设近地点A距地面高度为h,飞船在预定圆轨道上飞行n圈所用的时间为t,地球表面的重力加速度为g,地球半径R,试求:查看答案和解析>>
科目:高中物理 来源: 题型:
 “神舟七号”飞船完成了预定空间科学和技术实验任务后,返回舱于2008年9月28日17时37分开始从太空向地球表面按预定轨道返回,在离地10km 的高度打开阻力降落伞减速下降,这一过程中若返回舱所受阻力与速度的平方成正比,比例系数(空气阻力系数)为k.设返回舱总质量M=3000kg,所受空气浮力恒定不变,且认为竖直降落.从某时刻开始计时.返回舱的运动v--t图象如图中的AD曲线所示,图中AB是曲线在A点的切线,切线交于横轴一点B的坐标为(8,0),CD是平行横轴的直线,交纵轴于C点,c的坐标为(0,8).g取10m/s2,请回答下列问题:
“神舟七号”飞船完成了预定空间科学和技术实验任务后,返回舱于2008年9月28日17时37分开始从太空向地球表面按预定轨道返回,在离地10km 的高度打开阻力降落伞减速下降,这一过程中若返回舱所受阻力与速度的平方成正比,比例系数(空气阻力系数)为k.设返回舱总质量M=3000kg,所受空气浮力恒定不变,且认为竖直降落.从某时刻开始计时.返回舱的运动v--t图象如图中的AD曲线所示,图中AB是曲线在A点的切线,切线交于横轴一点B的坐标为(8,0),CD是平行横轴的直线,交纵轴于C点,c的坐标为(0,8).g取10m/s2,请回答下列问题:查看答案和解析>>
科目:高中物理 来源: 题型:阅读理解

查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com