
 如图所示,为氢原子的能级图.若在气体放电管中,处于基态的氢原子受到能量为12.8eV的高速电子轰击而跃迁到激发态,在这些氢原子从激发态向低能级跃迁的过程中( )
如图所示,为氢原子的能级图.若在气体放电管中,处于基态的氢原子受到能量为12.8eV的高速电子轰击而跃迁到激发态,在这些氢原子从激发态向低能级跃迁的过程中( )| A. | 最多能辐射出10种不同频率的光子 | |
| B. | 最多能辐射出6种不同频率的光子 | |
| C. | 能辐射出的波长最长的光子是从n=5跃迁到n=4能级时放出的 | |
| D. | 能辐射出的波长最长的光子是从n=4跃迁到n=3能级时放出的 |
分析 基态的氢原子受到能量为12.8eV的高速电子轰击,确定出氢原子处于哪一个能级,然后根据数学组合公式得出最多辐射光子频率的种数.激发态不稳定,向基态跃迁,能级差最小的,辐射光子频率最小,波长最长.
解答 解:A、根据-13.6+12.8eV=-0.8eV,知跃迁到第4能级,根据${C}_{4}^{2}$=6,知最多辐射出6种不同频率的光子.故A错误,B正确.
C、处于第4能级不稳定,向基态跃迁,由n=4跃迁到n=3,辐射的光子能量最小,频率最小,则波长最长.故C错误,D正确.
故选:BD.
点评 解决本题的关键知道吸收光子跃迁与电子轰击跃迁不同,吸收光子跃迁吸收的能量必须等于能级差,才能发生跃迁,而电子轰击不同,可以是一部分能量用来跃迁,一部分能量转化为电子的动能.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:多选题
| A. | 同一物体在星球表面受到的重力增大到原来的4倍 | |
| B. | 同一物体在星球表面受到的重力增大到原来的16倍 | |
| C. | 星球的第一宇宙速度增大到原来的4倍 | |
| D. | 星球的第一宇宙速度增大到原来的2倍 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
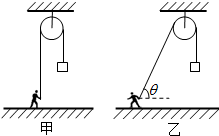 如图所示,某人通过定滑轮将一重物提升.第一次,此人竖直向下拉绳(甲图),使物体匀速上升高度h,该过程人对物体做功为W.第二次,此人拉着绳从定滑轮正下方以速度v匀速向左运动(乙图),使物体上升相同的高度,此时绳子与水平方向的夹角为θ,已知重力加速度为g.则第二次人对物体做的功为( )
如图所示,某人通过定滑轮将一重物提升.第一次,此人竖直向下拉绳(甲图),使物体匀速上升高度h,该过程人对物体做功为W.第二次,此人拉着绳从定滑轮正下方以速度v匀速向左运动(乙图),使物体上升相同的高度,此时绳子与水平方向的夹角为θ,已知重力加速度为g.则第二次人对物体做的功为( )| A. | W+$\frac{{W{v^2}{{sin}^2}θ}}{2gh}$ | B. | W+$\frac{{W{v^2}{{cos}^2}θ}}{2gh}$ | C. | W | D. | W-$\frac{{W{v^2}{{cos}^2}θ}}{2gh}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,内径均匀的U型玻璃管竖直放置,管右侧上端封闭,左侧上端开口,内有用细线栓住的活塞.两管中分别封人L=11cm的空气柱A和B,活塞上、下气体压强均等于76cm水银柱产生的压强,这时两管内的水银面的高度差h=6cm,现将活塞用细线缓慢地向上拉,使两管内水银面相平.求活塞向上移动的距离是多少?
如图所示,内径均匀的U型玻璃管竖直放置,管右侧上端封闭,左侧上端开口,内有用细线栓住的活塞.两管中分别封人L=11cm的空气柱A和B,活塞上、下气体压强均等于76cm水银柱产生的压强,这时两管内的水银面的高度差h=6cm,现将活塞用细线缓慢地向上拉,使两管内水银面相平.求活塞向上移动的距离是多少?查看答案和解析>>
科目:高中物理 来源: 题型:选择题
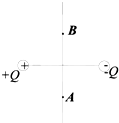 如图所示,一电子在力F作用下(力F未画出)沿等量异种电荷的中垂线由A向B做匀速直线运动,电子重力不计,则力F的大小和方向的变化情况是( )
如图所示,一电子在力F作用下(力F未画出)沿等量异种电荷的中垂线由A向B做匀速直线运动,电子重力不计,则力F的大小和方向的变化情况是( )| A. | 先变大后变小,方向水平向右 | B. | 先变大后变小,方向水平向左 | ||
| C. | 先变小后变大,方向水平向左 | D. | 先变小后变大,方向水平向右 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,直线a为电源的U-I图线,直线b为电阻R的U-I图线,当用该电源和该电阻组成闭合电路时,电源的总功率和电源的效率分别为( )
如图所示,直线a为电源的U-I图线,直线b为电阻R的U-I图线,当用该电源和该电阻组成闭合电路时,电源的总功率和电源的效率分别为( )| A. | 4W 33.3% | B. | 6W 33.3% | C. | 4W 66.7% | D. | 6W 66.7% |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 对于同一种气体,温度越高,分子平均动能越大 | |
| B. | 随着分子间的距离增大,分子势能一定增大 | |
| C. | 要使气体的分子平均动能增大,外界必须向气体传递热量 | |
| D. | 一定质量的气体,压强不变、温度升高时,分子间的平均距离一定增大 | |
| E. | 热量可能从低温物体向高温物体传递 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 研究加速度与合力、质量的关系 | B. | 建立“点电荷”的概念 | ||
| C. | 建立“瞬时速度”的概念 | D. | 建立“合力与分力”的概念 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com