
 ��ͼ��ʾ��������ľ��B����ˮƽ���ϣ�С����A����ľ��B���Ҷˣ�B���ϱ�����A֮��Ķ�Ħ��������1=0.2���±�����ˮƽ��Ķ�Ħ��������2=0.05�������Ħ�����뻬��Ħ������ȣ���ľ��B������mB=1.0kg��С����A����mA=0.60kg��t=0ʱ�̣�С����A��B��������Ե�����ٶ�vA=1.6m/s�����˶���ͬʱ��B����Ե�����ٶ�vB=0.40m/s�����˶����ʣ�gȡ10m/s2��
��ͼ��ʾ��������ľ��B����ˮƽ���ϣ�С����A����ľ��B���Ҷˣ�B���ϱ�����A֮��Ķ�Ħ��������1=0.2���±�����ˮƽ��Ķ�Ħ��������2=0.05�������Ħ�����뻬��Ħ������ȣ���ľ��B������mB=1.0kg��С����A����mA=0.60kg��t=0ʱ�̣�С����A��B��������Ե�����ٶ�vA=1.6m/s�����˶���ͬʱ��B����Ե�����ٶ�vB=0.40m/s�����˶����ʣ�gȡ10m/s2������ ��1���ֱ�����������������������ţ�ٵڶ����ɿ�������������Ӧ�ļ��ٶȣ�
��2�������ȱ���ֱ���˶����ɼ����з�������ȷ�������˶����λ�ƺ�ʱ���ϵ���Ӷ�������λ�ƣ����ɹ��Ĺ�ʽ�����Ħ���������Ĺ���
��� �⣺��1����ţ�ٵڶ�����F��=ma��
A�տ�ʼ�˶�ʱ�ļ��ٶȴ�С${a_A}=\frac{f_1}{m}=\frac{{{��_1}{m_A}g}}{m_A}=2.0m/{s^2}$������ˮƽ����
B�տ�ʼ�˶�ʱ��A��B��Ħ������СΪ${f_1}^'={f_1}={��_1}{m_A}g=1.2N$
�ܵ����B��Ħ����f2=��2��mA+mB��g=0.8N
B�տ�ʼ�˶�ʱ�ļ��ٶȴ�С${a_B}=\frac{{{F^'}+f}}{m_B}=2.0m/{s^2}$������ˮƽ����
��2����B�ӿ�ʼ�ȼ��ٵ����ʱ��Ϊt1������${t_1}=\frac{v_B}{a_B}=0.2s$
��ʱ����B�˶���λ��${s_{B1}}=\frac{{{v_B}{t_1}}}{2}=0.04m$
t1ʱ��A���ٶ�vA1=vA-aAt1=1.2m/s��0��
�ʴ˹���Aһֱ�ȼ����˶���
��t1ʱ����A�˶���λ��${s_{A1}}=\frac{{��{v_A}+{v_{A1}}��{t_1}}}{2}=0.28m$
��t1ʱ����A���B�˶���λ��s1=sA1+sB1=0.32m
t1ʱ���ڵ���Ħ������B���Ĺ�Ϊw1=-f2•sB1=-0.032J
t1������${f_1}^'��{f_2}$��B��ʼ�������ȼ����˶���A�������ȼ����˶����������ٶ����ʱA��B�Ҷ������Զ����˹����˶�ʱ��Ϊt2��A��B����ʱ�ٶ�Ϊv������
��A �ٶ�v=vA1-aAt2
��B ���ٶ�${a_{B1}}=\frac{{{f_1}^'-{f_2}}}{m_B}=0.4m/{s^2}$
�ٶ�v=aB1t2
�������ϸ�ʽ���������ݽ��v=0.2m/s��t=0.5s
t2ʱ����A�˶���λ��${s_{A2}}=\frac{{��v+{v_{A1}}��{t_2}}}{2}=0.35m$
t2ʱ����B�˶���λ��${s_{B2}}=\frac{{v{t_2}}}{2}=0.05m$
t2ʱ����A���B�˶���λ��s2=sA2-sB2=0.30m
t2ʱ���ڵ���Ħ������B���Ĺ�Ϊw1=-f2•sB2=-0.04J
����A��Զ�ܵ���a�㣬a��ľ���Ҷ˵ľ���LΪL=s1+s2=0.62m
��t=0ʱ�̵�A�˶���b��ʱ������Ħ������B���Ĺ�Ϊwf=w1+w2=-0.072J
�𣺣�1��A�ļ��ٶȴ�СΪ2.0m/s2������ˮƽ���ң�B�ļ��ٶȴ�СΪ2.0m/s2������ˮƽ����
��2����A�����B�ϵ��£���Զ�ܵ���ľ��B�ϵ�a�㣬a��ľ���Ҷ˵ľ���Ϊ0.62m����t=0ʱ����A�˶���a��ʱ������Ħ������B���Ĺ�Ϊ-0.072J��
���� ���⿼��ţ�ٵڶ����ɡ��˶�ѧ�����Լ����ļ������⣬Ҫע����ȷѡ���о�����������������������ȷѡ������������⼴�ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
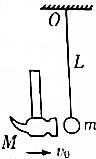 ��ͼ��ʾ�����������������ܳ��ܵ��������F=10N���������m=0.5kg��L=0.3m����ͷ������M=0.866kg���������ˮƽ���������m������ͷ���ٶȶ��ʱ���ܰ�����ϣ�����mԭ���Ǿ�ֹ�ģ������ͷ�Ǿ�ֹ�ģ�ȡg=10m/s2��
��ͼ��ʾ�����������������ܳ��ܵ��������F=10N���������m=0.5kg��L=0.3m����ͷ������M=0.866kg���������ˮƽ���������m������ͷ���ٶȶ��ʱ���ܰ�����ϣ�����mԭ���Ǿ�ֹ�ģ������ͷ�Ǿ�ֹ�ģ�ȡg=10m/s2���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
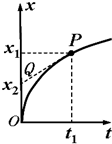 ��ͼ��ʾ��һ���ȱ���ֱ���˶����ʵ��λ��-ʱ��ͼ��x-tͼ��P��t1��x1��Ϊͼ����һ�㣮PQΪ��P������ߣ���x�ύ�ڵ�Q��������˵����ȷ���ǣ�������
��ͼ��ʾ��һ���ȱ���ֱ���˶����ʵ��λ��-ʱ��ͼ��x-tͼ��P��t1��x1��Ϊͼ����һ�㣮PQΪ��P������ߣ���x�ύ�ڵ�Q��������˵����ȷ���ǣ�������| A�� | t1ʱ�̣��ʵ������Ϊ$\frac{{x}_{1}}{{t}_{1}}$ | |
| B�� | t1ʱ�̣��ʵ������Ϊ$\frac{{x}_{1}-{x}_{2}}{{t}_{1}}$ | |
| C�� | �ʵ�ļ��ٶȴ�СΪ$\frac{{x}_{1}-{x}_{2}}{{t}_{1}^{2}}$ | |
| D�� | 0-t1ʱ���ڣ��ʵ��ƽ���ٶȴ�СΪ$\frac{2��{x}_{1}-{x}_{2}��}{{t}_{1}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��˹�ط����˵����Ĵ�ЧӦ | |
| B�� | ţ�ٽ����������糡�IJ���ԭ�� | |
| C�� | �����ڷ����˵�Ÿ�Ӧ���� | |
| D�� | ����ҵ����жϸ�Ӧ��������ķ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
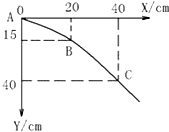 �������о�ƽ��������˶���ʵ��ʱ
�������о�ƽ��������˶���ʵ��ʱ�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
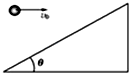 ��ͼ��ʾ�����Ϊ�ȵ�б�����Ϸ���һС���Գ��ٶ�v0ˮƽ�׳�����С��б���λ����С���������ٶ�Ϊg�������ʱ��tΪ��������
��ͼ��ʾ�����Ϊ�ȵ�б�����Ϸ���һС���Գ��ٶ�v0ˮƽ�׳�����С��б���λ����С���������ٶ�Ϊg�������ʱ��tΪ��������| A�� | $t=\frac{{{v_0}tan��}}{g}$ | B�� | t=$\frac{2{v}_{0}cot��}{g}$ | C�� | t=$\frac{{v}_{0}cot��}{g}$ | D�� | t=$\frac{2{v}_{0}tan��}{g}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
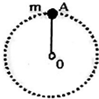 ����Ϊ0.5m������ϸ��OA��A����һ����Ϊ3kg��С����OΪԲ�ģ�����ֱƽ������Բ���˶�����ͼ��ʾ��С��ͨ����ߵ�ʱ���ٶ�Ϊ2m/s��ȡg=10m/s2�����ʱ���OA����������
����Ϊ0.5m������ϸ��OA��A����һ����Ϊ3kg��С����OΪԲ�ģ�����ֱƽ������Բ���˶�����ͼ��ʾ��С��ͨ����ߵ�ʱ���ٶ�Ϊ2m/s��ȡg=10m/s2�����ʱ���OA����������| A�� | �ܵ�6.0N������ | B�� | �ܵ�24N������ | C�� | �ܵ�6.0N��ѹ�� | D�� | �ܵ�54N������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
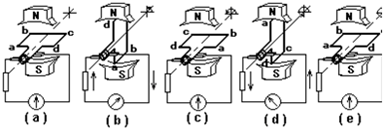
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com