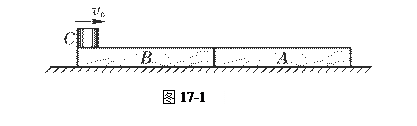
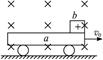
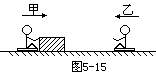
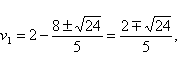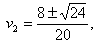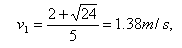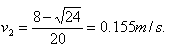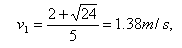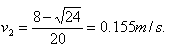先假设小物块C在木板B上移动x距离后,停在B上.这时A、B、C三者的速度相等,设为v,由动量守恒得
mv
0=(m+2M)v, ①
在此过程中,木板B的位移为s,小物块C的位移为s+x.由功能关系得
-μmg(s+x)=(1/2)mv
2-(1/2)mv
02,
μmgs=2Mv
2/2,
则 -μmgx=(1/2)(m+2M)v
2-(1/2)mv
02,②
由①、②式,得
x=[mv
02/(2M+m)μg], ③
代入数值得 x=1.6m. ④
x比B板的长度大.这说明小物块C不会停在B板上,而要滑到A板上.设C刚滑到A板上的速度为v
1,此时A、B板的速度为v
2,则由动量守恒得
mv
0=mv
1+2Mv
2, ⑤
由功能关系,得(1/2)mv
02-(1/2)mv
12-2×(1/2)mv
22=μmgL,
以题给数据代入,得
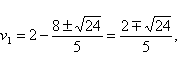
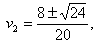
由v
1必是正值,故合理的解是
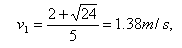
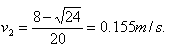
当滑到A之后,B即以v
2=0.155m/s做匀速运动,而C是以v
1=1.38m/s的初速在A上向右运动.设在A上移动了y距离后停止在A上,此时C和A的速度为v
3,由动量守恒得
Mv
2+mv
1=(m+M)v
3,
解得 v
3=0.563m/s.
由功能关系得
(1/2)mv
12+(1/2)mv
22-(1/2)(m+M)v
32=μmgy,
解得 y=0.50m.
y比A板的长度小,所以小物块C确实是停在A板上.最后A、B、C的速度分别为v
A=v
3=0.563m/s,v
B=v
2=0.155m/s,v
C=v
A=0.563m/s.
评分标准 本题的题型是常见的碰撞类型,考查的知识点涉及动量守恒定律与动能关系或动力学和运动学等重点知识的综合,能较好地考查学生对这些重点知识的掌握和灵活运动的熟练程度.题给数据的设置不够合理,使运算较复杂,影响了学生的得分.从评分标准中可以看出,论证占的分值超过本题分值的50%,足见对论证的重视.而大部分学生在解题时恰恰不注重这一点,平时解题时不规范,运算能力差等,都是本题失分的主要原因.
解法探析 本题参考答案中的解法较复杂,特别是论证部分,①、②两式之间的两个方程可以省略.下面给出两种较为简捷的论证和解题方法.
解法一 从动量守恒与功能关系直接论证求解.设C刚滑到A板上的速度为v
1,此时A、B板的速度为v
2,则由动量守恒,得?
mv
0=mv
1+2Mv
2,
以系统为对象,由功能关系,得
1/2)mv
02-(1/2)mv
12-2×(1/2)mv
22=μmgL,
由于v
1只能取正值,以题给数据代入得到合理的解为
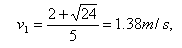
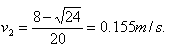
由于小物块C的速度v
1大于A、B板的速度v
2,这说明小物块C不会停在B板上.
以上过程既是解题的必要部分,又作了论证,比参考答案中的解法简捷.后面部分与参考答案相同,不再缀述.
解法二 从相对运动论证,用动量守恒与功能关系求解.
以地面为参照系,小物块C在A、B上运动的加速度为a
C=μg=1m/s
2,A、B整体的加速度为a
AB=μmg/2M=0.25m/s
2,C相对A、B的加速度a=a
C+a
AB=1.25m/s
2.假设A、B一体运动,以A、B整体为参照物,当C滑至与整体相对静止时,根据运动学公式,有
v
02=2as,
解得 s=v
02/2a=1.6m>L.
说明小物块C不会停在B板上.