
分析 飞船在离地面高度为h的圆形轨道上,飞行n圈,所用时间为t,可以求出飞船的周期,然后利用万有引力提供向心力列式可求质量,从而求密度
解答 解:设飞船的质量为m,地球的质量为M,在圆轨道上运行周期为T,飞船绕地球做匀速圆周运动,
由万有引力定律和牛顿第二定律得
G$\frac{Mm}{(R+h)^{2}}$=m(R+h)$\frac{4{π}^{2}}{{T}^{2}}$ ①
由题意得T=$\frac{t}{n}$ ②
解得地球的质量M=$\frac{4{n}^{2}{π}^{2}(R+h)^{3}}{G{t}^{2}}$ ③
又地球体积V=$\frac{4}{3}$πR3 ④
所以,地球的平均密度ρ=$\frac{M}{V}$=$\frac{3π{n}^{2}(R+h)^{3}}{G{t}^{2}{R}^{3}}$
答:地球的质量为$\frac{4{n}^{2}{π}^{2}(R+h)^{3}}{G{t}^{2}}$,平均密度$\frac{3π{n}^{2}(R+h)^{3}}{G{t}^{2}{R}^{3}}$
点评 解决天体问题重点是抓住万有引力提供向心力,向心力根据已知条件,选择合适公式,一切问题均迎刃而解


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中物理 来源: 题型:填空题
 在边长为L的正方形四个顶点A、B、C、D上依次放置电荷量为-q、-q、-q、+q的点电荷,则正方形中心O点的场强大小为$\frac{4kq}{{L}^{2}}$,方向D→B.
在边长为L的正方形四个顶点A、B、C、D上依次放置电荷量为-q、-q、-q、+q的点电荷,则正方形中心O点的场强大小为$\frac{4kq}{{L}^{2}}$,方向D→B.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
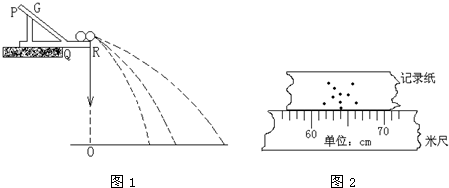
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 如图传送带保持1m/s运动,现将某0.5kg的小物体从左端放上,设物体与皮带间动摩擦因数为0.1,AB长为2.5m,则求物体从A到B的时间为3S.
如图传送带保持1m/s运动,现将某0.5kg的小物体从左端放上,设物体与皮带间动摩擦因数为0.1,AB长为2.5m,则求物体从A到B的时间为3S.查看答案和解析>>
科目:高中物理 来源: 题型:多选题

| A. | 物体做匀变速直线运动 | |
| B. | 在第3s内速度与加速度方向相同 | |
| C. | 在t=2s时,物体距出发点最远 | |
| D. | 物体先沿负方向运动,在t=2s后开始沿正方向运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
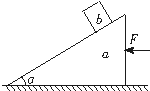 如图所示,质量为M的三角形木块a放在水平面上,把另一质量为m的木块b放在a的斜面上,斜面倾角为α,对a施一水平力F,使b不沿斜面滑动,不计一切摩擦,则b对a的压力大小为( )
如图所示,质量为M的三角形木块a放在水平面上,把另一质量为m的木块b放在a的斜面上,斜面倾角为α,对a施一水平力F,使b不沿斜面滑动,不计一切摩擦,则b对a的压力大小为( )| A. | $\frac{mg}{cosα}$ | B. | $\frac{Mg}{cosα}$ | C. | $\frac{FM}{(M+m)cosα}$ | D. | $\frac{Fm}{(M+m)sinα}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com