
 ��ͼ��ʾ��ˮƽ�����ϵĵ��ɾ���ϵ��Ϊk��һ�˹̶�����ֱǽ���ϣ���һ����һ����Ϊm�����壨�ɿ����ʵ㣩�����ӣ�������ˮƽ���Ķ�Ħ������Ϊ�̣����ƶ����彫���ɴ�ԭ��ѹ��x0��ֹ�ͷţ���ѧ�о��������ɵĵ��������뵯���쳤���Ĺ�ϵΪEp=$\frac{1}{2}$kx2���������Ħ�������ڻ���Ħ�������������ٶ�Ϊg����������ˮƽ�����˶�������
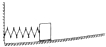
��ͼ��ʾ��ˮƽ�����ϵĵ��ɾ���ϵ��Ϊk��һ�˹̶�����ֱǽ���ϣ���һ����һ����Ϊm�����壨�ɿ����ʵ㣩�����ӣ�������ˮƽ���Ķ�Ħ������Ϊ�̣����ƶ����彫���ɴ�ԭ��ѹ��x0��ֹ�ͷţ���ѧ�о��������ɵĵ��������뵯���쳤���Ĺ�ϵΪEp=$\frac{1}{2}$kx2���������Ħ�������ڻ���Ħ�������������ٶ�Ϊg����������ˮƽ�����˶����������� ��1������Ep=$\frac{1}{2}$kx2����ⵯ�ɴ��浯������Ep��
��2�������״λָ�ԭ��ʱ���������غ����������ٶ�v��
��3����ȫ����ʹ�ö��ܶ������ɽ��
��� �⣺��1��������ѹ����Ϊx0ʱ���ɴ��浯������ Ep=$\frac{1}{2}$kx02��
��2�����ͷŵ������״λָ�ԭ�����������غ�ɵã�
Ep=��mgx0+$\frac{1}{2}m{v}^{2}$
��� v=$\sqrt{\frac{k{x}_{0}^{2}}{m}-2��g{x}_{0}}$
��3������������ͣ��ԭ��λ�ã������˶���·������������غ�ã�Ep=��mgs���
��ã�s���=$\frac{k{x}_{0}^{2}}{2��mg}$
����������ͣ�ڵ��ɵ����������Ħ������λ�ã������˶���·����С����ã�Ep=��mgs��С+$\frac{1}{2}k{x}^{2}$
�� x=$\frac{��mg}{k}$
��ã�s��С=$\frac{k{x}_{0}^{2}}{2��mg}$-$\frac{��mg}{2k}$
�������ͨ��·�̵ķ�ΧΪ��$\frac{k{x}_{0}^{2}}{2��mg}$-$\frac{��mg}{2k}$��s��$\frac{k{x}_{0}^{2}}{2��mg}$��
��
��1��������ѹ����Ϊx0ʱ���ɴ��浯������EpΪ$\frac{1}{2}$kx02��
��2���������ָܻ�ԭ�������״λָ�ԭ��ʱ������ٶ�vΪ$\sqrt{\frac{k{x}_{0}^{2}}{m}-2��g{x}_{0}}$��
��3���������ͨ��·�̵ķ�ΧΪ��$\frac{k{x}_{0}^{2}}{2��mg}$-$\frac{��mg}{2k}$��s��$\frac{k{x}_{0}^{2}}{2��mg}$��
���� ��������Ϣ�⣬����Ҫ���������⣬֪�����������뵯�ɵ��α����Ĺ�ϵ�����Ҫ�������������ת���ģ����������غ㶨�ɽ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
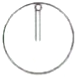 һ���һ�˹̶�����Ϊm��С������һ��OΪԲ�ģ�ʹС������ֱƽ�������뾶ΪR��Բ���˶�����ͼ��ʾ��������
һ���һ�˹̶�����Ϊm��С������һ��OΪԲ�ģ�ʹС������ֱƽ�������뾶ΪR��Բ���˶�����ͼ��ʾ��������| A�� | С���˶��������ܵ����������������������� | |
| B�� | С�����ߵ�ʱ����С�ٶ���$\sqrt{gR}$ | |
| C�� | С�����ߵ�ʱ���˶�������������������������������෴����ʱ����һ�����ڸ˶���������� | |
| D�� | С�����͵�ʱ����Ը˵�����һ������������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
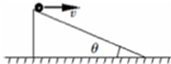 ��ͼ��ʾ��С������Ϊ��=30���б�����׳��������ڸ�б���ϣ�����֪С����ƽ���˶��ij�����Ϊ6J�������������ƣ������䵽б����ʱ�Ķ���Ϊ��������
��ͼ��ʾ��С������Ϊ��=30���б�����׳��������ڸ�б���ϣ�����֪С����ƽ���˶��ij�����Ϊ6J�������������ƣ������䵽б����ʱ�Ķ���Ϊ��������| A�� | 10J | B�� | 12J | C�� | 14J | D�� | 8J |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ţ�ٵ�һ������ͨ��ʵ��ó��� | |
| B�� | ����������Ĺ������ԣ��ٶȴ���������һ���� | |
| C�� | ţ������ͨ������б��ʵ��ó�������ά�������˶��ı�Ȼ��� | |
| D�� | ���Ǹı������˶�״̬��ԭ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ѡ��ͬ�IJο�ƽ�棬��ÿ���������������ܵ��������ܲ���ͬ | |
| B�� | ����ѡʲô�ο�ƽ�棬������ĩ״̬���������ܶ���� | |
| C�� | ѡ��ͬ�IJο�ƽ�棬�ڸ���������������� | |
| D�� | ѡ��ͬ�IJο�ƽ�棬�ڸ�������������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
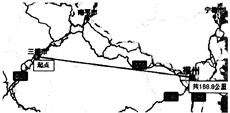 ��ͼ��ʾ����ij���Լݻ�У�ij������8��00��ʼ��������G70�ݳ�ǰ�����ݣ�����11��00���︣�ݣ���֪ȫ�̹�·���Լ270���ֱ�߾���168.8��������й��������ڴ˹����е��˶�����������ǣ�������
��ͼ��ʾ����ij���Լݻ�У�ij������8��00��ʼ��������G70�ݳ�ǰ�����ݣ�����11��00���︣�ݣ���֪ȫ�̹�·���Լ270���ֱ�߾���168.8��������й��������ڴ˹����е��˶�����������ǣ�������| A�� | 8��00��ָһ��ʱ�� | |
| B�� | ������ʻ��ƽ��������90km/h | |
| C�� | ������ʻ��λ�ƴ�С��168.8���� | |
| D�� | �о������ڵ�ͼ�ϵ��˶��켣ʱ���ɿ����ʵ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �����˶������е�ǣ�������� | |
| B�� | �������ܴﵽ������ٶ�Ϊ40m/s | |
| C�� | �����ٶ�Ϊ10m/sʱ�����ٶ���2m/s2 | |
| D�� | �����˶������м��ٶȲ��������ٶ�Ҳ��������ֱ������������˶� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ����Ϊ2kg�����徲ֹ���㹻���ˮƽ���ϣ�����������Ķ�Ħ������Ϊ0.2�����Ħ�����ͻ���Ħ������С��Ϊ��ȣ���t=0ʱ�̿�ʼ�������ܵ����䡢��С�������Ա仯��ˮƽ����F�����ã�F��ʱ��t�ı仯������ͼ��ʾ��ȡ�������ٶ�g=10m/s2����������t=0��t=6s���ʱ���ڵ�λ�ƴ�СΪ��������
����Ϊ2kg�����徲ֹ���㹻���ˮƽ���ϣ�����������Ķ�Ħ������Ϊ0.2�����Ħ�����ͻ���Ħ������С��Ϊ��ȣ���t=0ʱ�̿�ʼ�������ܵ����䡢��С�������Ա仯��ˮƽ����F�����ã�F��ʱ��t�ı仯������ͼ��ʾ��ȡ�������ٶ�g=10m/s2����������t=0��t=6s���ʱ���ڵ�λ�ƴ�СΪ��������| A�� | 4 m | B�� | 8 m | C�� | 10m | D�� | 12m |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ֻҪ����������������������һ���仯 | |
| B�� | ����������ֱ���˶�ʱ������������һ������ | |
| C�� | ��������Ϊ0�����壬�����ܶԱ���������� | |
| D�� | ij�����崦��ij��λ�ã����������ܵ�ֵ��Ψһȷ���� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com