
 如图所示,由半径为R的$\frac{3}{4}$光滑圆周和倾角为45°的光滑斜面组成的轨道固定在竖直平面内,斜面和圆周之间由小圆弧平滑连接.一小球恰能过最高点,并始终贴着轨道内侧顺时针转动.则小球通过斜面的时间为(重力加速度为g)( )
如图所示,由半径为R的$\frac{3}{4}$光滑圆周和倾角为45°的光滑斜面组成的轨道固定在竖直平面内,斜面和圆周之间由小圆弧平滑连接.一小球恰能过最高点,并始终贴着轨道内侧顺时针转动.则小球通过斜面的时间为(重力加速度为g)( )| A. | 2$\sqrt{gR}$ | B. | 2$\sqrt{\frac{R}{g}}$ | C. | (2$\sqrt{2}$-2)$\sqrt{\frac{R}{g}}$ | D. | ($\sqrt{10}$-$\sqrt{6}$)$\sqrt{\frac{R}{g}}$ |
分析 分析小球在光滑轨道上滑行,顺时针从内侧通过斜面,从题条件可知,小球在斜面上做匀加速直线运动,因为加速度恒定,初速度越小通过斜面的时间越长,根据小球在圆周轨道内侧能做圆周运动的条件判断到达斜面项端时小球的最小速度,从而再根据运动学求出小球运动的时间即可.
解答 解:如图,小球能在圆周内侧斜面做圆周运动,通过圆周最高点的速度$v≥\sqrt{gR}$,则根据动能定理,可求出小球到达斜面顶端时的速度v1,有:
mgR=$\frac{1}{2}m{v}_{1}^{2}-\frac{1}{2}m{v}^{2}$
可得:${v}_{1}=\sqrt{{v}^{2}+2gR}$
要求小球通过斜面时间最长,要求v1尽可能小,根据速度$v≥\sqrt{gR}$的条件可知,v1的最小值等于${v}_{1}=\sqrt{3gR}$
物体在光滑斜面上下滑时,沿斜面下滑的加速度a=gsinθ=$\frac{\sqrt{2}}{2}g$,已知小球在斜面上做匀加速运动的初速度${v}_{1}=\sqrt{3gR}$,加速度a=$\frac{\sqrt{2}}{2}g$,位移x=$\sqrt{2}R$,根据运动学公式可以求出小球通过斜面的最长时间为:
t=$(\sqrt{10}-\sqrt{6})\sqrt{\frac{R}{g}}$,故D正确.
故选:D
点评 解决本题的关键是认识小球能圆内侧轨道做圆周运动时能过通过最高点的条件是$v≥\sqrt{gR}$从而得求小球滑上斜面时的最小速度,再根据运动学公式求出最小时间.


科目:高中物理 来源: 题型:选择题
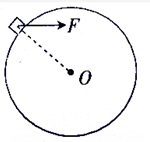
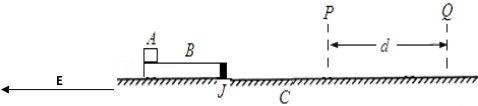
| A. | 物块受到的支持逐渐增大 | B. | 物块受到的支持力先减小后增大 | ||
| C. | 拉力F逐渐减小 | D. | 拉力F先增大后减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
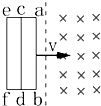 如图所示矩形金属框架的三条竖直边ab、cd、ef长均为L,电阻都为R,其余电阻不计,框架以速度v匀速地进入磁感应强度为B的匀强磁场中,设ab、cd、ef三条边先后进入磁场时,ab边两端的电压分别为U1,U2,和U3,则( )
如图所示矩形金属框架的三条竖直边ab、cd、ef长均为L,电阻都为R,其余电阻不计,框架以速度v匀速地进入磁感应强度为B的匀强磁场中,设ab、cd、ef三条边先后进入磁场时,ab边两端的电压分别为U1,U2,和U3,则( )| A. | U1=$\frac{BLv}{3}$ | B. | U2=2U1 | C. | U3=0 | D. | U1=U2=U3 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
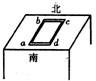 根据地磁场的特征可知,在北半球的地磁场有一水平向北的分量Bx和一个竖直向下的分量By,某研究性小组设计了如图所示实验测量Bx和By的大小,将一个电阻为R的长方形线圈abcd沿着磁针所指的南北方向平放在北半球的一个水平桌面上,测得线圈两边的长度为ab=L1,bc=L2,现突然将线圈翻转180°,使ab边与dc边互换位置,用冲击电流计测得线圈中流过的电荷量为q1,然后维持bc边不动,将线圈绕bc边转动,使线圈突然竖直,这次测得线圈中流过的电荷量为q2,则( )
根据地磁场的特征可知,在北半球的地磁场有一水平向北的分量Bx和一个竖直向下的分量By,某研究性小组设计了如图所示实验测量Bx和By的大小,将一个电阻为R的长方形线圈abcd沿着磁针所指的南北方向平放在北半球的一个水平桌面上,测得线圈两边的长度为ab=L1,bc=L2,现突然将线圈翻转180°,使ab边与dc边互换位置,用冲击电流计测得线圈中流过的电荷量为q1,然后维持bc边不动,将线圈绕bc边转动,使线圈突然竖直,这次测得线圈中流过的电荷量为q2,则( )| A. | By=$\frac{R{q}_{1}}{{L}_{1}{L}_{2}}$ | B. | By=$\frac{R{q}_{1}}{2{L}_{1}{L}_{2}}$ | ||
| C. | Bx=$\frac{R(2{q}_{2}+{q}_{1})}{2{L}_{1}{L}_{2}}$ | D. | Bx=$\frac{R(2{q}_{2}-{q}_{1})}{2{L}_{1}{L}_{2}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
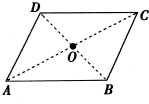 在一匀强电场区域中,有A、B、C、D四点恰好位于一平行四边形的四个顶点上,如图所示,O点为平行四边形两条对角线的交点,已知:φA=-4V,φB=6V,φC=8V,则D、O两点电势φD的为-2V,φO的为2V.
在一匀强电场区域中,有A、B、C、D四点恰好位于一平行四边形的四个顶点上,如图所示,O点为平行四边形两条对角线的交点,已知:φA=-4V,φB=6V,φC=8V,则D、O两点电势φD的为-2V,φO的为2V.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
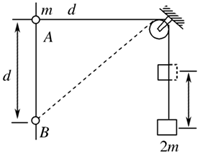 如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )
如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )| A. | 环到达B处时,重物上升的高度h=$\sqrt{2}d$ | |
| B. | 环到达B处时,环与重物的速度大小满足${v_物}=\sqrt{2}{v_环}$ | |
| C. | 环到达B,重物的速度大小${v_物}=\frac{{\sqrt{(6-4\sqrt{2})gd}}}{2}$ | |
| D. | 环从A到达B的过程中,环克服轻绳拉力做的功($\sqrt{2}$-1)mgd |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
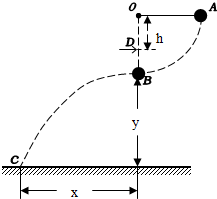 质量为m=0.5kg的小球用长为?的细线悬挂于O点,在O的正下方h=1.2m的D处有一刀口向右的刀片,现把小球拉到A处,使OA呈水平状态,无初速放手后小球摆到B处,由于细线被割断,小球水平飞出,下落y=5m后刚好落到地面上,水平射程x=6m,试求
质量为m=0.5kg的小球用长为?的细线悬挂于O点,在O的正下方h=1.2m的D处有一刀口向右的刀片,现把小球拉到A处,使OA呈水平状态,无初速放手后小球摆到B处,由于细线被割断,小球水平飞出,下落y=5m后刚好落到地面上,水平射程x=6m,试求查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 斥力,大小$\frac{4k{Q}^{2}}{{d}^{2}}$ | B. | 斥力,大小$\frac{16k{Q}^{2}}{{d}^{2}}$ | ||
| C. | 引力,大小$\frac{4k{Q}^{2}}{{d}^{2}}$ | D. | 引力,大小$\frac{32k{Q}^{2}}{{d}^{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com