
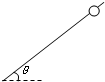
 有一质量为2kg的小球串在长为1m的轻杆顶部,轻杆与水平方向成θ=37°角.
有一质量为2kg的小球串在长为1m的轻杆顶部,轻杆与水平方向成θ=37°角.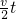 得 v=
得 v=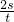 =
=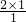 m/s=2m/s
m/s=2m/s =2m/s2,
=2m/s2, =20N
=20N 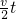 求出小球到达杆底时速率,由P=mg?vsin53°求出重力的功率.
求出小球到达杆底时速率,由P=mg?vsin53°求出重力的功率. 求出小球下滑的加速度,由牛顿第二定律和摩擦力公式求解小球与轻杆之间的动摩擦因数.
求出小球下滑的加速度,由牛顿第二定律和摩擦力公式求解小球与轻杆之间的动摩擦因数.

科目:高中物理 来源: 题型:
 如图,一质量为M的长木板静止在水平面上,有一质量为m的小滑块以一定的水平速度冲上木板,已知滑块和木板之间的动摩擦因数为μ0,最大静摩擦力等于滑动摩
如图,一质量为M的长木板静止在水平面上,有一质量为m的小滑块以一定的水平速度冲上木板,已知滑块和木板之间的动摩擦因数为μ0,最大静摩擦力等于滑动摩查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
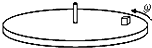 (2013?如东县模拟)如图所示,在可绕中心轴转动的水平圆盘上,有一质量m=2kg的小滑块,离转轴的距离r=0.2m,与圆盘间的最大静摩擦力Fm=10N.
(2013?如东县模拟)如图所示,在可绕中心轴转动的水平圆盘上,有一质量m=2kg的小滑块,离转轴的距离r=0.2m,与圆盘间的最大静摩擦力Fm=10N.查看答案和解析>>
科目:高中物理 来源: 题型:
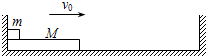
 (2013?怀远县模拟)如图所示,在光滑水平面上有一质量为M的长木板,长木板上有一质量为m的小物块,它与长木板间的动摩擦因数为μ.开始时,长木板与小物块均靠在与水平面垂直的固定挡板处,某时刻它们以共同的速度v0向右运动,当长木板与右边的固定竖直挡板碰撞后,其速度的大小不变、方向相反,以后每次的碰撞均如此.设左右挡板之间的距离足够长,且M>m.
(2013?怀远县模拟)如图所示,在光滑水平面上有一质量为M的长木板,长木板上有一质量为m的小物块,它与长木板间的动摩擦因数为μ.开始时,长木板与小物块均靠在与水平面垂直的固定挡板处,某时刻它们以共同的速度v0向右运动,当长木板与右边的固定竖直挡板碰撞后,其速度的大小不变、方向相反,以后每次的碰撞均如此.设左右挡板之间的距离足够长,且M>m.查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,质量M=2kg的长木板静止放在光滑水平面上,在木板左端放有一质量m=2kg的小滑块(可视为质点),木板与滑块之间动摩擦因数均为μ=0.2.现在让滑块获得水平向右的速度v1=3m/s,同时木板获得水平向左的速度v2=1m/s.(g=10m/s2)求:
如图所示,质量M=2kg的长木板静止放在光滑水平面上,在木板左端放有一质量m=2kg的小滑块(可视为质点),木板与滑块之间动摩擦因数均为μ=0.2.现在让滑块获得水平向右的速度v1=3m/s,同时木板获得水平向左的速度v2=1m/s.(g=10m/s2)求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com