
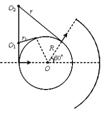
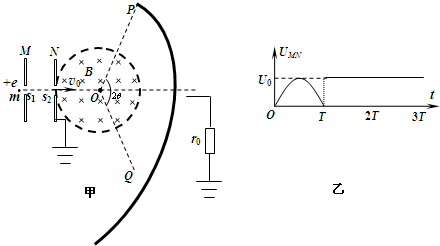
如图甲所示,M、N为竖直放置的两块平行金属板,圆形虚线为与N相连且接地的圆形金属网罩。PQ为与圆形网罩同心的金属收集屏,通过阻值为r0的电阻与大地相连。小孔s1、s2、圆心O与PQ中点位于同一水平线上。圆心角2θ=120°、半径为R的网罩内有大小为B,方向垂直纸面向里的匀强磁场。M、N间相距![]() 且接有如图乙所示的随时间t变化的电压,
且接有如图乙所示的随时间t变化的电压,![]() (0
(0![]() t
t![]() T),
T),![]() (t >T)(式中
(t >T)(式中![]() ,T已知),质量为m、电荷量为e的质子连续不断地经s1进入M、N间的电场,接着通过s2进入磁场。(质子通过M、N的过程中,板间电场可视为恒定,质子在s1处的速度可视为零,质子的重力及质子间相互作用均不计。)
,T已知),质量为m、电荷量为e的质子连续不断地经s1进入M、N间的电场,接着通过s2进入磁场。(质子通过M、N的过程中,板间电场可视为恒定,质子在s1处的速度可视为零,质子的重力及质子间相互作用均不计。)
(1)质子在哪些时间段内自s1处进入板间,穿出磁场后均能打到收集屏PQ上?
(2)质子从进入s1到穿出金属网罩经历的时间记为![]() ,写出
,写出![]() 与UMN之间的函数关系(tanx=a 可表示为x=arctana)
与UMN之间的函数关系(tanx=a 可表示为x=arctana)
(3)若毎秒钟进入s1的质子数为n,则收集屏PQ电势稳定后的发热功率为多少?
 |
解:
(1)质子在板间运动,根据动能定理,有![]()
![]() (1分)
(1分)
质子在磁场中运动,根据牛顿第二定律,有![]()
![]() (1分)
(1分)
若质子能打在收集屏上,轨道半径![]() 与半径
与半径![]() 应满足的关系:
应满足的关系:![]() (1分)
(1分)
解得板间电压![]() (1分)
(1分)
结合图象可知:质子在![]()
![]() t
t![]()
![]() 和t
和t![]() T之间任一时刻从s1处进入电场,均能打到
T之间任一时刻从s1处进入电场,均能打到
收集屏上 (2分)
(2)M、N间的电压越小,质子穿出电场进入磁场时的速度越小,质子在极板间经历的时间越长,同时在磁场中运动轨迹的半径越小,在磁场中运动的时间也会越长,设在磁场中质子运动所对应的圆半径为r,运动圆弧所对应的圆心角为![]() ,射出电场的速度为v0,质子穿出金属网罩时,对应总时间为t,则
,射出电场的速度为v0,质子穿出金属网罩时,对应总时间为t,则
在板间电场中运动时间![]() (2分)
(2分)
![]()
![]() (1分)
(1分)
在磁场中运动时间![]() (1分)
(1分)
所以,运动总时间![]() =
=![]() +
+![]()
![]() (1分)
(1分)
![]() 在磁场中运动时间(1分)
在磁场中运动时间(1分)
所以,运动总时间![]() =
=![]()
![]() (2分)
(2分)
(3)稳定时, 收集屏上电荷不再增加,即在t>T 时刻以后,此时,![]() ,收集屏与地面电势差恒为U,U=Ir0
,收集屏与地面电势差恒为U,U=Ir0
单位时间到达收集板的质子数n
单位时间内,质子的总能量为![]() (2分)
(2分)
单位时间内屏上发热功率为![]() (2分)
(2分)
消耗在电阻上的功率为![]() (2分)
(2分)
所以收集板发热功率 ![]() (2分)
(2分)


科目:高中物理 来源: 题型:

查看答案和解析>>
科目:高中物理 来源: 题型:
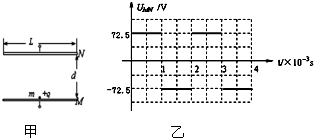 如图甲所示,M、N为水平放置的平行板电容器的两极板,极板长L=0.2m,两板间距d=0.145m,在M、N间加上如图乙所示的电压,一个带电粒子的电量q=+1.0×10-6C、质量m=1.0×10-8kg,粒子重力不计.
如图甲所示,M、N为水平放置的平行板电容器的两极板,极板长L=0.2m,两板间距d=0.145m,在M、N间加上如图乙所示的电压,一个带电粒子的电量q=+1.0×10-6C、质量m=1.0×10-8kg,粒子重力不计.查看答案和解析>>
科目:高中物理 来源: 题型:
| R |
| 2 |
| π |
| T |
| 3eB2R2 |
| m |
查看答案和解析>>
科目:高中物理 来源: 题型:
 (2012?嘉兴二模)如图甲所示,M、N为竖直放置的两块平行金属板,圆形虚线为与N相连且接地的圆形金属网罩.PQ为与圆形网罩同心的金属收集屏,通过阻值为r0的电阻与大地相连.小孔s1、s2、圆心O与PQ中点位于同一水平线上.圆心角2θ=120°、半径为R的网罩内有大小为B,方向垂直纸面向里的匀强磁场.M、N间相距
(2012?嘉兴二模)如图甲所示,M、N为竖直放置的两块平行金属板,圆形虚线为与N相连且接地的圆形金属网罩.PQ为与圆形网罩同心的金属收集屏,通过阻值为r0的电阻与大地相连.小孔s1、s2、圆心O与PQ中点位于同一水平线上.圆心角2θ=120°、半径为R的网罩内有大小为B,方向垂直纸面向里的匀强磁场.M、N间相距| R |
| 2 |
| π |
| T |
| 3eB2R2 |
| m |
查看答案和解析>>
科目:高中物理 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com