
 游乐场中有一类似于过山车的设施.简易模型如图所示,它由倾角为α=37°的光滑斜面轨道、水平轨道和竖直平面内的光滑圆形轨道组成,A、B分别是斜面与圆形轨道的最低点(且A处有一极小光滑圆弧与轨道相切),A、B两点相距L=4.25m.一个质量为m=0.1kg的小球(视为质点),从斜面上距A点h=4.05m高处由静止下滑,小球与水平轨道的动摩擦因数μ=0.2.假设水平轨道足够长,不考虑斜面轨道与圆形轨道相互重叠时对小球运动的影响,sin37°=0.6,g取lOm/s2.求:
游乐场中有一类似于过山车的设施.简易模型如图所示,它由倾角为α=37°的光滑斜面轨道、水平轨道和竖直平面内的光滑圆形轨道组成,A、B分别是斜面与圆形轨道的最低点(且A处有一极小光滑圆弧与轨道相切),A、B两点相距L=4.25m.一个质量为m=0.1kg的小球(视为质点),从斜面上距A点h=4.05m高处由静止下滑,小球与水平轨道的动摩擦因数μ=0.2.假设水平轨道足够长,不考虑斜面轨道与圆形轨道相互重叠时对小球运动的影响,sin37°=0.6,g取lOm/s2.求:分析 (1)对小球的运动过程进行分析,运用动能定理求出最高点时的速度,并利用牛顿第二定律求出轨道对小球作用力;
(2)知道小球恰能通过圆形轨道的含义,再应用动能定理研究整个过程求出两种情况下的问题,再求小球最终停留点与B点的距离.
解答 解:(1)由动能定理,有mgh-μmgL=$\frac{1}{2}$mvB2
代入数据解得:vB=8.0m/s
由牛顿第二定律得:FN-mg=m$\frac{{v}_{B}^{2}}{R}$
代入数据解得:FN=7.4N
由牛顿第三定律得,小球到达B点时对轨道的压力大小${F}_{N}^{′}$=FN=7.4N
(2)要保证小球不脱离轨道,可分两种临界情况进行讨论:
Ⅰ.轨道半径较小时,小球恰能通过圆形轨道,设在最高点的速度为v,应满足
由牛顿第二定律得:mg=m$\frac{{v}^{2}}{{R}_{1}}$
由功能关系得:$\frac{1}{2}$mvB2=mg•R1+$\frac{1}{2}$mv2
代入数据解得:R1=1.28m
Ⅱ.轨道半径较大时,小球上升的最大高度为R2,
根据机械能守恒:$\frac{1}{2}$mvB2=mg•R2
代入数据解得:R2=3.2 m
综合Ⅰ、Ⅱ,要使小球不脱离轨道,则圆形轨道的半径须满足下面的条件
0<R≤1.28 m或R≧3.2m
当0<R≤1.28 m时,小球最终停留点与B点的距离为L',则:-μmgL′=0-$\frac{1}{2}$mvB2
解得:L'=16.0 m
当R≧3.2m时,小球最终停留点与B点的距离为L″,则
L″=L-(L'-3L)=1.0 m
答:(1)小球到达B点时的速度大小为8.0m/s;对轨道的压力大小为7.4N;
(2)欲使小球不脱离轨道,在圆形轨道的设计中,半径应满足的条件是0<R≤1.28 m或R≧3.2m;小球最终停留点与B点的距离为1.0 m.
点评 选取研究过程,运用动能定理解题.动能定理的优点在于适用任何运动包括曲线运动.知道小球恰能通过圆形轨道的含义以及要使小球不能脱离轨道的含义.


科目:高中物理 来源: 题型:多选题
 一列简谐横波沿直线传播,以波源O由平衡位置开始振动为计时零点,质点A的振动图象如图所示,已知O、A的平衡位置相距1.2m.以下判断正确的是( )
一列简谐横波沿直线传播,以波源O由平衡位置开始振动为计时零点,质点A的振动图象如图所示,已知O、A的平衡位置相距1.2m.以下判断正确的是( )| A. | 波速大小为0.4m/s | B. | 波源起振方向沿y轴正方向 | ||
| C. | 质点A在一个周期向前运动了1.6m | D. | 质点A的动能在t=5s时最大 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 一定是直线运动 | B. | 一定是曲线运动 | ||
| C. | 可能是直线运动,可能是曲线运动 | D. | 一定不是曲线运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,一物体在沿斜面向上的恒力F作用下,由静止从底端沿光滑的斜面向上做匀加速直线运动,经过一段时间恒力F对物体做功为60J,此后撤掉力F,物体又回到出发点,在整个运动过程中下列说法正确的是( )
如图所示,一物体在沿斜面向上的恒力F作用下,由静止从底端沿光滑的斜面向上做匀加速直线运动,经过一段时间恒力F对物体做功为60J,此后撤掉力F,物体又回到出发点,在整个运动过程中下列说法正确的是( )| A. | 撤去外力时,物体的动能为60 J | |
| B. | 物体运动到最高点的过程中,重力做功为60 J | |
| C. | 物体回到出发点时,物体的动能为60 J | |
| D. | 物体回到出发点时,重力的功率出现最大值 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 运动物体所受的合力不为零,合力必做功,物体的动能一定要变化 | |
| B. | 运动物体所受的合力为零,则物体的动能一定不变 | |
| C. | 运动物体的动能保持不变,则该物体所受合力一定为零 | |
| D. | 运动物体所受合力不为零,则该物体一定做变速运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
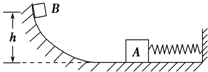 如图所示,轻质弹簧的一端固定在墙上,另一端与质量为m的物体A相连,A放在光滑水平面上,有一质量与A相同的物体B,从高h处由静止开始沿光滑曲面滑下,与A相碰后一起将弹簧压缩,弹簧复原过程中某时刻B与A分开且沿原曲面上升.下列正确的是( )
如图所示,轻质弹簧的一端固定在墙上,另一端与质量为m的物体A相连,A放在光滑水平面上,有一质量与A相同的物体B,从高h处由静止开始沿光滑曲面滑下,与A相碰后一起将弹簧压缩,弹簧复原过程中某时刻B与A分开且沿原曲面上升.下列正确的是( )| A. | 弹簧被压缩时所具有的最大弹性势能为mgh | |
| B. | 弹簧被压缩时所具有的最大弹性势能为$\frac{mgh}{2}$ | |
| C. | B能达到的最大高度为$\frac{h}{2}$ | |
| D. | B能达到的最大高度为$\frac{h}{4}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
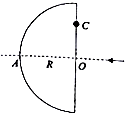 如图所示是一个半径为R的半球形透明物体的侧视图,现在有一细束单色光沿半径OA方向入射,保持入射方向不变,不考虑光线在透明物体内部的反射.
如图所示是一个半径为R的半球形透明物体的侧视图,现在有一细束单色光沿半径OA方向入射,保持入射方向不变,不考虑光线在透明物体内部的反射.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
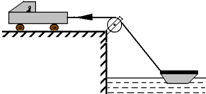 如图所示,汽车在河岸上通过细绳拖船靠岸,绕过滑轮的两段绳子在同一个竖直平面内,滑轮可视为质点,如果汽车牵引绳子匀速前进,则被拖的船将做( )
如图所示,汽车在河岸上通过细绳拖船靠岸,绕过滑轮的两段绳子在同一个竖直平面内,滑轮可视为质点,如果汽车牵引绳子匀速前进,则被拖的船将做( )| A. | 匀速运动 | B. | 加速运动 | ||
| C. | 减速运动 | D. | 无法确定是加速还是减速的运动 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com