
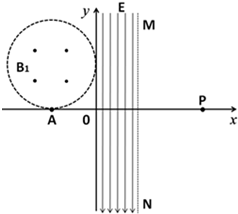
 ��ͼ��ʾ���ڶ����ޣ��뾶Ϊr��Բ�������ڴ��ڷ���ֱֽ���������ǿ�ų����ų��߽�ǡ���������������У�x�����е�A����һ����Դ���ܹ���x���Ϸ�����������ȣ���Ϊv������Ϊm������Ϊ+q�����ӣ������������ƣ�Բ������ų��ĴŸ�Ӧǿ��B1=$\frac{mv}{qr}$��y���Ҳ�0��y��r�ķ�Χ�ڴ�����y�Ḻ�������ǿ�糡����֪ij���Ӵ�A����+y��������ų����ٽ�����ǿ�糡���������Ӵӵ糡�ұ߽�MN������ٶȷ�����x���������45���б���£���
��ͼ��ʾ���ڶ����ޣ��뾶Ϊr��Բ�������ڴ��ڷ���ֱֽ���������ǿ�ų����ų��߽�ǡ���������������У�x�����е�A����һ����Դ���ܹ���x���Ϸ�����������ȣ���Ϊv������Ϊm������Ϊ+q�����ӣ������������ƣ�Բ������ų��ĴŸ�Ӧǿ��B1=$\frac{mv}{qr}$��y���Ҳ�0��y��r�ķ�Χ�ڴ�����y�Ḻ�������ǿ�糡����֪ij���Ӵ�A����+y��������ų����ٽ�����ǿ�糡���������Ӵӵ糡�ұ߽�MN������ٶȷ�����x���������45���б���£������� ��1�������ڵ糡������ƽ���˶�������ƽ���˶��ֽ�Ϊx�����y����ķ��˶����Է��˶�����ţ�ٵڶ����ɽ���˶�ѧ���ɼ������E��
��2�������ڴų���������Բ���˶�����ţ�ٵڶ����ɵõ��켣�뾶���ɼ��ι�ϵ�����������Ŀ��ȣ��Ӷ����Բ����ǿ�ų�B2����С�뾶��
��3�����ݻ��������ٶȴ�С֮���������ڴų����˶�ʱ�䣮�ɷ��˶���λ�ƹ�ʽ��糡���˶�ʱ�䣮�õ������������˶���ʱ�䣬�������˶��Ĺ������ʱ�䣬�Ӷ��õ���ʱ�䣮
��� �⣺
��1���裺��������ƽ���˶���ˮƽλ�ƴ�СΪx����ֱ������ٶȴ�СΪvy����ƽ�ļ��ٶȴ�СΪa����ƽ��ʱ��Ϊt
����ţ�ٵڶ�����Eq=ma����a=$\frac{qE}{m}$
�����ڵ糡������ƽ���˶���������ƽ�Ĺ����У�
x����x=vt=r
y����vy=at=$\frac{qE}{m}$t=$\frac{Eqr}{mv}$
���Ӵӵ糡�ұ߽�MN������ٶȷ�����x���������45��б���£��� vy=v��
��������ǿ�糡�ĵ糡ǿ�ȴ�СE=$\frac{{mv}^{2}}{qr}$
��2�������ڴų���������Բ���˶�����ţ�ٵڶ����ɵ�
qVB1=m$\frac{{v}^{2}}{R}$
����������֪B1=$\frac{mv}{qr}$
�� R=r
��Ϊ�ų��뾶��켣�뾶��ͬ�����������뿪�ų�����ٶȷ������+x����
���������Ӵ�����ǿ�糡���ٶ�����ƫ���� y=$\frac{1}{2}$at2=$\frac{1}{2}$r�����
�����Ӵ�MN�������ߵ�ΪE����͵�ΪF����EF=2r
�����������Ŀ��� d=$\sqrt{2}$r
Բ����ǿ�ų�B2����С�뾶 rB2=$\frac{\sqrt{2}}{2}$r
��3�������ڴų�B1���˶�ʱ�� t1=$\frac{l}{v}$=$\frac{��r}{2v}$
��������ǿ�糡���˶�ʱ�� t2=$\frac{r}{v}$ ���������˶��ٶ� v��=$\sqrt{2}$v
���������˶��ľ��� x3=$\frac{\sqrt{2}}{2}$r
���������˶���ʱ�� t3=$\frac{{x}_{3}}{v��}$=$\frac{r}{2v}$
�����ڴų�B2���˶�ʱ�� t4=$\frac{��r}{4v}$
��������A���˶���x���ϵ�P�����ʱ�� t=t1+t2+t3+t4=$\frac{3r}{2v}$+$\frac{3��r}{4v}$
�𣺣�1����ǿ�糡�ĵ糡ǿ�ȴ�СΪ$\frac{{mv}^{2}}{qr}$
��2��Բ����ǿ�ų�B2����С�뾶Ϊ$\frac{\sqrt{2}}{2}$r
��3��������A���˶���x���ϵ�P�����ʱ��Ϊ$\frac{3r}{2v}$+$\frac{3��r}{4v}$
���� ���⿼�����������ƫת�糡�е���ƽ���˶����Լ������������н�ų����˶�ʱ���н�ų�����С��������⣮�����Զ࣬Ҫ��ϸ�������㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ����糡��ų�������ͬ���෴����������ӵĶ�������һ���ı� | |
| B�� | ����糡��ų�������ͬ���෴����������ӵĶ���һ���ı� | |
| C�� | ����������ӵĶ����ķ��ֲ��䣬��糡��ų�����һ�����ഹֱ | |
| D�� | ����������ӵĶ��ܱ��ֲ��䣬��糡��ų�����һ�����ഹֱ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
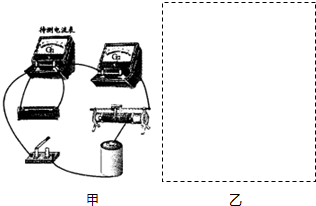 ijѧϰС��������ͼ��ʾ��ʵ���·������ʵ�ʵ�����G1������r1�Ĵ�С����Ҫ�����������ȷ���һ������������ڷ��㣮
ijѧϰС��������ͼ��ʾ��ʵ���·������ʵ�ʵ�����G1������r1�Ĵ�С����Ҫ�����������ȷ���һ������������ڷ��㣮�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
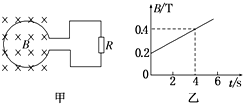 ��ͼ��ʾ��һ��Բ����Ȧ������n=100����Ȧ���S=200cm2����Ȧ�ĵ���r=1������Ȧ���һ����ֵR=4���ĵ��裬����Ȧ����һ����ֱ��Ȧƽ���������ǿ�ų��У��Ÿ�Ӧǿ����ʱ��仯������ͼ����ʾ������˵������ȷ���ǣ�������
��ͼ��ʾ��һ��Բ����Ȧ������n=100����Ȧ���S=200cm2����Ȧ�ĵ���r=1������Ȧ���һ����ֵR=4���ĵ��裬����Ȧ����һ����ֱ��Ȧƽ���������ǿ�ų��У��Ÿ�Ӧǿ����ʱ��仯������ͼ����ʾ������˵������ȷ���ǣ�������| A�� | ��Ȧ�еĸ�Ӧ��������Ϊ��ʱ�뷽�� | |
| B�� | ����R���˵ĵ�ѹ��ʱ��������� | |
| C�� | ��Ȧ����r���ĵĹ���Ϊ4��10-4 W | |
| D�� | ǰ4 s��ͨ��R�ĵ����Ϊ4��10-4 C |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
 ijͬѧ����ֱ���ҵĵ����¼ӹҹ��룬��ʵ���о������뵯���쳤���Ĺ�ϵ���±��Ǹ�ͬѧ��ʵ�����ݣ�ʵ��ʱ����ʼ��δ���������ȣ����ɺ��ᣬ�����������Բ��ƣ�gȡ10m/s2
ijͬѧ����ֱ���ҵĵ����¼ӹҹ��룬��ʵ���о������뵯���쳤���Ĺ�ϵ���±��Ǹ�ͬѧ��ʵ�����ݣ�ʵ��ʱ����ʼ��δ���������ȣ����ɺ��ᣬ�����������Բ��ƣ�gȡ10m/s2| ��������m/g | 0 | 30 | 60 | 90 | 120 | 150 |
| �����ܳ���L/cm | 6.0 | 7.2 | 8.3 | 9.5 | 10.6 | 11.8 |
| ����F/N | ||||||
| �����쳤x/m |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
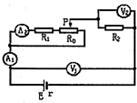 ��ͼ��ʾ�ĵ�·�У���Դ���費�ܺ��ԣ�R1����ֵС�ڻ���������R0�������裬��ѹ������������������ģ����������Ļ���ͷP�ɱ��������е�������ƶ��Ĺ����У�������
��ͼ��ʾ�ĵ�·�У���Դ���費�ܺ��ԣ�R1����ֵС�ڻ���������R0�������裬��ѹ������������������ģ����������Ļ���ͷP�ɱ��������е�������ƶ��Ĺ����У�������| A�� | A1��ʾ�����ϼ�С | B�� | A2��ʾ���������� | ||
| C�� | V1��ʾ���ȱ�С���� | D�� | V2��ʾ���ȱ����С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��������һ�պϵ�·�Ĵ�ͨ�������� | |
| B�� | ��������һ�պϵ�·�Ĵ�ͨ���ı仯�������� | |
| C�� | ��������һ�պϵ�·�Ĵ�ͨ���ı仯�ʳ����� | |
| D�� | ��������һ�պϵ�·�ĴŸ�Ӧǿ�ȳ����� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
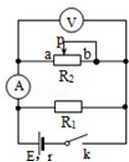 ��ͼ��ʾ��R1Ϊ��ֵ���裬R2Ϊ�����ֵΪ2R1�Ŀɱ���裬EΪ��Դ�綯�ƣ�rΪ��Դ���裬��СΪr=R1����R2�Ļ���P��a����b�Ĺ����У�����˵������ȷ���ǣ�������
��ͼ��ʾ��R1Ϊ��ֵ���裬R2Ϊ�����ֵΪ2R1�Ŀɱ���裬EΪ��Դ�綯�ƣ�rΪ��Դ���裬��СΪr=R1����R2�Ļ���P��a����b�Ĺ����У�����˵������ȷ���ǣ�������| A�� | ��R2=$\frac{{R}_{1}}{2}$ʱ��R2�ϻ������� | |
| B�� | ��R2=R1ʱ��R2�ϻ������� | |
| C�� | ��ѹ��ʾ���͵�����ʾ��֮�������� | |
| D�� | ��ѹ��ʾ���͵�����ʾ��֮�ȱ��ֲ��� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com