
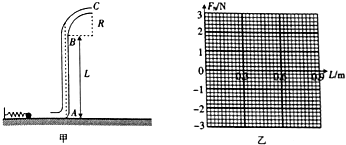
分析 (1)当L=0.1m时,根据功能原理求得小球弹射时弹簧对小球做的功.
(2)小球通过C时临界速度为$\sqrt{gR}$时,小球对管道壁没有作用力,大于临界速度时对上管壁有压力,小球临界速度时对下管壁有压力,根据动能定理求出经过C点的速度,根据牛顿第二定律求出管壁对球的作用力与长度L的关系,再画出图象.
解答 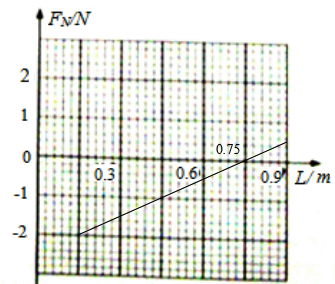 解:(1)当L=0.1 m时,由功能原理得:
解:(1)当L=0.1 m时,由功能原理得:
每次弹射时弹簧对小球所做的功 W=mg(L+R)+$\frac{1}{2}m{v}_{C}^{2}$
解得:W=0.6J;
(2)小球在C点处的向心力:mg-FN=m$\frac{{v}_{C}^{2}}{R}$
为使小球能到达C处,须满足:
W-mg(L+R)≥0
得 L≤0.9 m
所以FN=$\frac{10}{3}$L-$\frac{5}{2}$(N)(0.03m≤L≤0.9m)
FN随长度L变化的关系图线如上图所示;
答:
(1)每次弹射时弹簧对小球所做的功是0.6J.
(2)FN与L之间的关系式是FN=$\frac{10}{3}$L-$\frac{5}{2}$(N)(0.03m≤L≤0.9m),在图乙所示的坐标纸上作出FN随长度L变化的关系图线如图.
点评 本题考查了机械能守恒定律与平抛运动规律,掌握小球能过最高点的临界条件,注意掌握过最高点时的绳球模型和杆球模型临界条件的不同.


 名校课堂系列答案
名校课堂系列答案科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 当副线圈空载(断路)时,原线圈上的电压为零 | |
| B. | 原线圈的输入电压,随着副线圈中输出的电流的增大而增大 | |
| C. | 原线圈中输入的电流,随着副线圈中输出的电流的增大而增大 | |
| D. | 以上说法都不正确 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
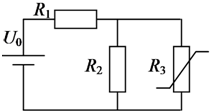 图中电源电压为U0=10V,内阻不计,电阻器R1和R2为已知的定值电阻,R1=R2=2Ω,R3为非线性元件,该元件的电流与电压关系为I=αU2(α=0.1A/V2为常数),则通过非线性元件的电流I=1.34A.
图中电源电压为U0=10V,内阻不计,电阻器R1和R2为已知的定值电阻,R1=R2=2Ω,R3为非线性元件,该元件的电流与电压关系为I=αU2(α=0.1A/V2为常数),则通过非线性元件的电流I=1.34A.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
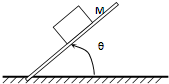 如图所示,物体M静止于倾斜放置的木板上,使木板的倾斜角θ缓慢增大至M开始滑动之前的过程中,下列说法中正确的是( )
如图所示,物体M静止于倾斜放置的木板上,使木板的倾斜角θ缓慢增大至M开始滑动之前的过程中,下列说法中正确的是( )| A. | 物体对木板的压力逐渐减小 | |
| B. | 物体所受摩擦力减小 | |
| C. | 物体所受支持力和摩擦力的合力变小 | |
| D. | 物体所受支持力和摩擦力的合力不变 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
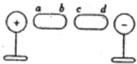 如图所示,在两个带等量异种电荷的绝缘导体球之间,对称地放着两个相同的导体必ab、cd,则:
如图所示,在两个带等量异种电荷的绝缘导体球之间,对称地放着两个相同的导体必ab、cd,则:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 此星球的半径R=$\frac{F{T}^{2}}{4m{π}^{2}-m{T}^{2}{ω}^{2}}$ | |
| B. | 此星球的平均密度ρ=$\frac{3π}{G{T}^{2}}$ | |
| C. | 星球自转角速度ω若变大,小球m在赤道上受到的重力为F也将变大 | |
| D. | 飞船要返回近地轨道,至少使飞船在赤道上获得$\frac{1}{2}$$\frac{m{ω}^{2}{F}^{2}{T}^{4}}{(4m{π}^{2}-m{T}^{2}{ω}^{2})^{2}}$的能量 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com