
| A. | 卫星的线速度为$\frac{\sqrt{2g{R}_{0}}}{2}$ | B. | 卫星的角速度是$\sqrt{\frac{g}{2{R}_{0}}}$ | ||
| C. | 卫星的向心加速度为$\frac{{g}_{0}}{2}$ | D. | 卫星的周期为4π$\sqrt{\frac{2{R}_{0}}{g}}$ |
分析 在球表面表面重力与万有引力相等,卫星圆周运动的向心力由万有引力提供据此由卫星的轨道半径分析计算即可.
解答 解:在地面重力与万有引力相等有:$G\frac{mM}{{R}_{0}^{2}}=mg$可得GM=$g{R}_{0}^{2}$
对距地面高度为R0的卫星轨道半径为2R0由万有引力公式有:
$G\frac{mM}{4{R}_{0}^{2}}=\frac{GMm}{4{R}_{0}^{2}}=\frac{1}{4}mg$
据万有引力提供圆周运动向心力有:
$\frac{1}{4}mg=m\frac{{v}^{2}}{2{R}_{0}}=m•2{R}_{0}{ω}^{2}=ma=m•2{R}_{0}\frac{4{π}^{2}}{{T}^{2}}$
A、可得线速度v=$\sqrt{\frac{1}{2}g{R}_{0}}$,故A正确;
B、可得角速度$ω=\sqrt{\frac{g}{8{R}_{0}}}$,故B错误;
C、可得向心加速度a=$\frac{1}{4}g$,故C错误;
D、可得周期T=4$π\sqrt{\frac{2{R}_{0}}{g}}$,故D正确.
故选:AD.
点评 解决本题的关键是抓住地球表面万有引力与重力相等,二是万有引力提供卫星圆周运动的向心力.


科目:高中物理 来源: 题型:解答题
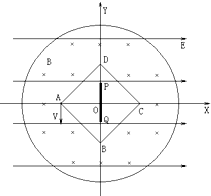 如图所示,在直角坐标系xoy平面内有沿x轴正方向的水平匀强电场,场强为E.在正方形ABCD(O为正方形的中心)与O为圆心半径为2L的圆形之间的区域加垂直纸面向里的匀强磁场,磁感应强度为B.在y轴上有一挡板PQ,挡板长为L,挡板的放置关于x轴对称.A为一个质子源,OA=L,可以向y轴负方向发射出速度从零开始的一系列质子,已知质子的质量为m,电量为q,质子的重力忽略不计.求:
如图所示,在直角坐标系xoy平面内有沿x轴正方向的水平匀强电场,场强为E.在正方形ABCD(O为正方形的中心)与O为圆心半径为2L的圆形之间的区域加垂直纸面向里的匀强磁场,磁感应强度为B.在y轴上有一挡板PQ,挡板长为L,挡板的放置关于x轴对称.A为一个质子源,OA=L,可以向y轴负方向发射出速度从零开始的一系列质子,已知质子的质量为m,电量为q,质子的重力忽略不计.求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
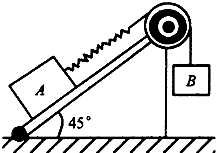 如图所示,物体A、B用细绳与弹簧连接后跨过滑轮.A静止在倾角为45°的粗糙斜面上,B悬挂着.已知质量mA=3mB,不计滑轮摩擦.现将斜面倾角由45°减小到30°,那么下列说法中正确的是( )
如图所示,物体A、B用细绳与弹簧连接后跨过滑轮.A静止在倾角为45°的粗糙斜面上,B悬挂着.已知质量mA=3mB,不计滑轮摩擦.现将斜面倾角由45°减小到30°,那么下列说法中正确的是( )| A. | 弹簧的弹力将减小 | B. | 细绳对滑轮的作用力将减小 | ||
| C. | 物体A受到的静摩擦力将减小 | D. | 地面对斜面体的摩擦力将减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
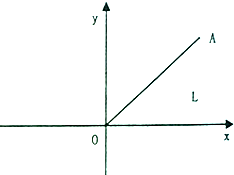 如图所示,质量为m,电荷量为+q的粒子从坐标原点O以初速度v0射出,粒子恰好经过A点,O、A两点长度为L,连线与坐标轴+y方向的夹角为α=45°,不计粒子的重力.
如图所示,质量为m,电荷量为+q的粒子从坐标原点O以初速度v0射出,粒子恰好经过A点,O、A两点长度为L,连线与坐标轴+y方向的夹角为α=45°,不计粒子的重力.查看答案和解析>>
科目:高中物理 来源: 题型:填空题
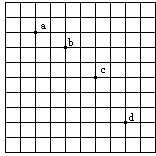 如图所示,在研究平抛运动的实验中,用一张印有小方路的记录轨迹,小方块的边长L=1.25cm,若小球在平抛运动图中的几个位置是a,b,c,d,则小球平抛的初速的计算式为v0=2$\sqrt{gL}$,小球在b点的速率是0.875m/s;若以a为坐标原点,水平向右为x轴正方向,竖直向下为y轴正方向,则小球的抛出点的坐标是(-0.0117m,-0.0013m).
如图所示,在研究平抛运动的实验中,用一张印有小方路的记录轨迹,小方块的边长L=1.25cm,若小球在平抛运动图中的几个位置是a,b,c,d,则小球平抛的初速的计算式为v0=2$\sqrt{gL}$,小球在b点的速率是0.875m/s;若以a为坐标原点,水平向右为x轴正方向,竖直向下为y轴正方向,则小球的抛出点的坐标是(-0.0117m,-0.0013m).查看答案和解析>>
科目:高中物理 来源: 题型:解答题
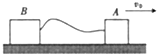 如图所示,光滑水平面上用轻质细绳相连的A、B两物体,它们的质量分别为mA=2kg和mB=1kg,开始时B静止,A以v0=3m/s的速度向右滑动,当细绳被拉直后,A和B一起以相同的速度向右运动,求:
如图所示,光滑水平面上用轻质细绳相连的A、B两物体,它们的质量分别为mA=2kg和mB=1kg,开始时B静止,A以v0=3m/s的速度向右滑动,当细绳被拉直后,A和B一起以相同的速度向右运动,求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,A、B两物块的质量分别为2m和m,静止地叠放在水平地面上,A、B间的动摩擦因数为μ,B与地面间的动摩擦因数为2μ,已知最大静摩擦力等于滑动摩擦力,重力加速度为g,现对A施加一水平拉力F(不为0),则( )
如图所示,A、B两物块的质量分别为2m和m,静止地叠放在水平地面上,A、B间的动摩擦因数为μ,B与地面间的动摩擦因数为2μ,已知最大静摩擦力等于滑动摩擦力,重力加速度为g,现对A施加一水平拉力F(不为0),则( )| A. | 只要F>2μmg,A就能被拉动 | |
| B. | 拉动A后,A、B间的摩擦力随F的增大而增大 | |
| C. | 无论F为何值,B都不会被拉动 | |
| D. | 只要F足够大,B就可能被拉动 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
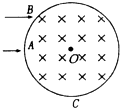 如图所示,在一个半径为R的圆形区域内存在垂直纸面向里的匀强磁场,O为圆心,一个电子以一定速度v沿AO方向(水平)射入磁场,经过时间t从O点正下方的C点射出磁场,另一电子以相同速度从磁场边界上的B点水平射入磁场,两速度方向与圆周在同一平面内,且A、B两点间圆弧长度为$\frac{π}{4}$R,则第二个电子在磁场中运动的时间为多少?
如图所示,在一个半径为R的圆形区域内存在垂直纸面向里的匀强磁场,O为圆心,一个电子以一定速度v沿AO方向(水平)射入磁场,经过时间t从O点正下方的C点射出磁场,另一电子以相同速度从磁场边界上的B点水平射入磁场,两速度方向与圆周在同一平面内,且A、B两点间圆弧长度为$\frac{π}{4}$R,则第二个电子在磁场中运动的时间为多少?查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,质量为m的小球与处于同一竖直平面内的三根相同的轻质弹簧相连,静止时相邻两弹簧间的夹角为120°,已知弹簧a、b对小球的作用力均为F,且F>mg,则竖直弹簧c对小球的作用力大小可能是( )
如图所示,质量为m的小球与处于同一竖直平面内的三根相同的轻质弹簧相连,静止时相邻两弹簧间的夹角为120°,已知弹簧a、b对小球的作用力均为F,且F>mg,则竖直弹簧c对小球的作用力大小可能是( )| A. | 2F | B. | F+mg | C. | F-mg | D. | mg-F |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com