

分析 (1)碰撞过程系统动量守恒、机械能守恒,碰撞后物体做匀变速直线运动,应用动量守恒定律与机械能守恒定律、运动学公式求出A、B、C的速度.
(2)应用能量守恒定律求出C向右运动的位移,然后求出碰撞次数.
(3)根据物体的运动情况,求出物体的位移.
解答 解:(1)设弹簧恢复原长时A、B两小球速度大小分别为vA、vB,系统动量时候,以A的初速度方向为正方向,由动量守恒定律得:
mvA=2mvB,
由机械能守恒定律得:EP=$\frac{1}{2}$mvA2+$\frac{1}{2}$•2mvB2,
解得:vA=2$\sqrt{\frac{μgL}{3}}$,
vB=$\sqrt{\frac{μgL}{3}}$,
小球A向左运动历时t1到达槽左端竖直壁处,则:L=vAt1,
解得:t1=$\frac{1}{2}$$\sqrt{\frac{3L}{μg}}$,
设小球A与槽左端竖直壁发生弹性碰撞后,小球A与木槽C速度大小分别为vA1、vC,
由于小球A与木槽C质量相等,速度交换,有:vA1=0,
木槽C以速度:vC=2$\sqrt{\frac{μgL}{3}}$,向左匀减速运动,
木槽C加速度大小为a,由牛顿第二定律得:4μmg=ma,
解得:a=4μg,
木槽C历时t2,速度减为零,vC=at2,
解得:t2=$\frac{1}{2}$$\sqrt{\frac{L}{3μg}}$,
向左位移大小:xC1,有:xC1=$\frac{{v}_{C}^{2}}{2a}$=$\frac{L}{6}$,
小球B在时间t1+t2内向右运动位移大小:xB=vB(t1+t2)=$\frac{2L}{3}$,
得木槽C速度减为零时,小球B与槽右端竖直壁距离$\frac{L}{6}$,
设小球B与槽右端竖直壁发生弹性碰撞后,小球B与木槽C速度大小分别为vB1、vC1,
系统动量守恒,以向右为正方向,由动量守恒定律得:2mvB1+mvC1=2mvB,
由机械能守恒定律得:$\frac{1}{2}$•2mvB12+$\frac{1}{2}$mvC12=$\frac{1}{2}$•2mvB2,
解得:vB1=$\frac{{v}_{B}}{3}$=$\frac{\sqrt{3μgL}}{9}$,vC1=$\frac{4{v}_{B}}{3}$=$\frac{4\sqrt{3μgL}}{9}$,
随后C水平向右以初速vC1作加速度为a匀减速直线运动,B以vB1水平向右作匀速直线运动,经分析可知:C先减速至停止,然后B再以速度vB1与C发生第二次碰撞,
设B与C发生第二次碰撞后瞬时,小球B与木槽C速度大小分别为vB2、vC2,以向右为正方向,由动量守恒定律得:
2mvB2+mvC2=2mvB1,
由机械能守恒定律得:$\frac{1}{2}$•2mvB22+$\frac{1}{2}$mvC22=$\frac{1}{2}$•2mvB12,
解得:vB2=$\frac{\sqrt{3μgL}}{27}$,vC2=$\frac{4\sqrt{3μgL}}{27}$,A的速度为0;
(2)由分析知:B与C将一直碰撞下去,直至最终B、C均停止,设C向右运动路程为x,C与水平桌面摩擦生热,由能量守恒定律得:
μ•4mg($\frac{L}{6}$+x)=EP=μmgL,
解得:x=$\frac{L}{12}$,
说明此后C、A不再碰撞,所以整个运动过程中,A球与槽左端竖直壁只发生1次碰撞;
(3)整个运动过程中,A位移大小:sA=L,方向水平向左,
B位移大小:sB=$\frac{11L}{12}$,方向水平向右,
C位移大小:sC=$\frac{L}{12}$,方向水平向左;
答:(1)B球与槽右端竖直壁发生第2次碰撞后瞬间,A、B、C三者各自速度大小分别为:0、$\frac{\sqrt{3μgL}}{27}$、$\frac{4\sqrt{3μgL}}{27}$;
(2)整个运动过程中,A与槽左端竖直壁发生碰撞的次数是1次;
(3)整个运动过程中,A、B、C三者各自相对地面的位移分别是:L、方向水平向左,$\frac{11L}{12}$、方向水平向右,$\frac{L}{12}$、方向水平向左.
点评 本题是一道力学综合题,难度较大,本题的难点在:分析清楚各物体的运动过程,分析清楚物体运动过程后,应用动量守恒定律、能量守恒定律、动能定律即可正确解题.


科目:高中物理 来源: 题型:选择题
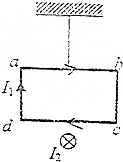 矩形线框abcd被一根细绳悬挂于天花板上,线框中通有如图所示的顺时针方向的电流I1,线框中心的正下方有一与线框平面垂直的长直导线,当导线中通入向里的电流I2时,关于线框运动及细绳拉力变化的判断正确的是( )
矩形线框abcd被一根细绳悬挂于天花板上,线框中通有如图所示的顺时针方向的电流I1,线框中心的正下方有一与线框平面垂直的长直导线,当导线中通入向里的电流I2时,关于线框运动及细绳拉力变化的判断正确的是( )| A. | 线框ad向里、bc向外转动,细绳的拉力增大 | |
| B. | 线框ad向里,bc向外转,细绳的拉力减小 | |
| C. | 线框ad向外,bc向里转动,细绳的拉力增大 | |
| D. | 线框ad向外,bc向里转动,细绳的拉力减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | 灯泡两端的电压与流过它的电流成正比 | |
| B. | 灯泡的电阻随温度的升高而增大 | |
| C. | 灯泡的电阻不变 | |
| D. | 灯泡的功率不变 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
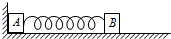 如图所示用轻弹簧连接放在光滑水平面上质量分别为m、M的木块A、B,m≠M,开始时A靠竖直墙,A、B均静止,弹簧处于自然长度.现对B施一水平外力使其向左缓慢移动,做功W后撤去水平外力,则在随后的运动过程中( )
如图所示用轻弹簧连接放在光滑水平面上质量分别为m、M的木块A、B,m≠M,开始时A靠竖直墙,A、B均静止,弹簧处于自然长度.现对B施一水平外力使其向左缓慢移动,做功W后撤去水平外力,则在随后的运动过程中( )| A. | 木块A、B系统动量守恒 | |
| B. | 木块A的最大速度为$\sqrt{\frac{2W}{m}}$ | |
| C. | 在木块A离开竖直墙后的运动过程中,弹簧的最大弹性势能为$\frac{mW}{m+M}$ | |
| D. | 在木块A离开竖直墙后的运动过程中,木块B一定始终向右运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 只有磁铁周围才存在磁场 | |
| B. | 磁场是假想的,不是客观存在的 | |
| C. | 磁场是在磁极与磁极、磁极和电流发生作用时才产生 | |
| D. | 磁感线是假想的,不存在的 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
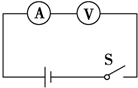 用两只完全相同的电流表分别改装成一只电流表和一只电压表.将它们串联起来接入电路中,如图所示,此时( )
用两只完全相同的电流表分别改装成一只电流表和一只电压表.将它们串联起来接入电路中,如图所示,此时( )| A. | 两只电表的指针偏转角相同 | |
| B. | 两只电表的指针偏转角不确定 | |
| C. | 电流表指针的偏转角小于电压表指针的偏转角 | |
| D. | 电流表指针的偏转角大于电压表指针的偏转角 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
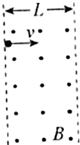 如图所示,一带电粒子的质量m=1.7×10-27kg,电荷量q=1.6×10-19C,以速度v=3.2×106m/s,沿着垂直于磁场方向,且垂直于磁场边界的方向射入匀强磁场中,已知磁场强度B=0.17T,磁场的宽度L=10cm,取g=10m/s2.
如图所示,一带电粒子的质量m=1.7×10-27kg,电荷量q=1.6×10-19C,以速度v=3.2×106m/s,沿着垂直于磁场方向,且垂直于磁场边界的方向射入匀强磁场中,已知磁场强度B=0.17T,磁场的宽度L=10cm,取g=10m/s2.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
| 整车行驶质量 | 1500kg |
| 额定功率 | 75kW |
| 加速过程 | 车辆从静止加速到30m/s所需时间为10s |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com