
���� ú��������ڴ��ʹ�������ٶ���ͬ������Դ��ʹ���ǰ���������˶�ѧ��ʽ������ٶ�ʱ��ͼ��������ι��������λ�ƵĴ�С���Ӷ��ó���ɫ�ۼ��ij���L0��
��� 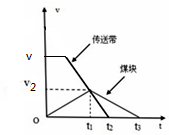 �⣺��1��ú����t=2sʱ���ٶȴ�С v1=a0t=2��2=4m/s
�⣺��1��ú����t=2sʱ���ٶȴ�С v1=a0t=2��2=4m/s
���˶�����������ʹ���ú���v-tͼ����ͼ��ʾ��
��ͼ�ɵã�v2=a0t1=v-a��t1-t��
���t1=$\frac{v+at}{{a}_{0}+a}$=$\frac{9+3��2}{2+3}$=3s
��ú�������������е�������� v2=a0t1=2��3=6m/s
��2�����ٶ����ǰ��ú������ڴ��ʹ��������ɫ�ۼ��ij���Ϊ
L1=[vt+$\frac{v+{v}_{2}}{2}��{t}_{1}-t��$]-$\frac{1}{2}$v2t1=16.5m
��ú���봫��������ٶ�����Ժ����߶����ȼ���ֱ���˶���ú������ڴ��ʹ�����ǰ������
���ߵij���Ϊ L2=$\frac{{v}_{2}^{2}}{2{a}_{0}}$-$\frac{{v}_{2}^{2}}{2a}$=3m
��ΪL1��L2���˺�ɫ�ۼ��ij��� L0=L1=16.5m
��
��1��ú����t=2sʱ���ٶȴ�Сv1Ϊ4m/s�������������е��������v2��6m/s��
��2���˺�ɫ�ۼ��ij���L0��16.5m��
���� �������Ĺؼ�����ú���ڴ��ʹ��ϵ��˶����ɣ����ţ�ٵڶ����ɺ��˶�ѧ��ʽ������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
 �Ⱥ��Ǹ��������о��������������ӵ�һ����Ҫ���������������������������������֮������ʾ���Ⱥ���ͬ�����Ӳ���һ����ͬһ�����ӣ���ͼ��ʾ���ڲⶨ���ӱȺɵ�ʵ���У���ƽ�н�����İ峤L=2��10-2 m��������d=2��10-2m��������ѹU=180V��һ������������v0=2��107 m/s���ٶȴ�ֱ�糡һ�������糡����ͼ��ʾ���뿪�糡ʱ��ƫ����y=5��10-3 m���������ӵ������������������ݣ���
�Ⱥ��Ǹ��������о��������������ӵ�һ����Ҫ���������������������������������֮������ʾ���Ⱥ���ͬ�����Ӳ���һ����ͬһ�����ӣ���ͼ��ʾ���ڲⶨ���ӱȺɵ�ʵ���У���ƽ�н�����İ峤L=2��10-2 m��������d=2��10-2m��������ѹU=180V��һ������������v0=2��107 m/s���ٶȴ�ֱ�糡һ�������糡����ͼ��ʾ���뿪�糡ʱ��ƫ����y=5��10-3 m���������ӵ������������������ݣ����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
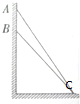 ��ͼ��ʾ��λ����ֱƽ���ڵ�һ��ľ��б������ֱǽ�ϵ�A�㣬����ˮƽ��ļн�Ϊ53�㣬��һͬ�����ϵij�ľ��б������ֱǽ�ϵ�B�㣬����ˮƽ��ļн�Ϊ45�㣬����ľ��˶���C�㴦������һС���A���ɾ�ֹ�ͷţ�С���˶���C����ʱΪt����ͬ-С���B���ɾ�ֹ�ͷţ�С���˶���C����ʱҲΪt����С���볤ľ���Ķ�Ħ������Ϊ��sin53��=0.8��cos53��=0.6����������
��ͼ��ʾ��λ����ֱƽ���ڵ�һ��ľ��б������ֱǽ�ϵ�A�㣬����ˮƽ��ļн�Ϊ53�㣬��һͬ�����ϵij�ľ��б������ֱǽ�ϵ�B�㣬����ˮƽ��ļн�Ϊ45�㣬����ľ��˶���C�㴦������һС���A���ɾ�ֹ�ͷţ�С���˶���C����ʱΪt����ͬ-С���B���ɾ�ֹ�ͷţ�С���˶���C����ʱҲΪt����С���볤ľ���Ķ�Ħ������Ϊ��sin53��=0.8��cos53��=0.6����������| A�� | $\frac{1}{7}$ | B�� | $\frac{3}{14}$ | C�� | $\frac{3\sqrt{2}}{8}$ | D�� | $\frac{5\sqrt{2}}{8}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
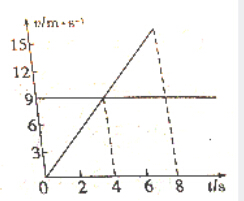 A��B���ʵ�ͬʱ����ͬһ�㣬��ͬһ������ֱ���˶������˶���v-tͼ����ͼ��ʾ�������ʵ��ٴ�������ʱ��t��������ǰ����������s�ֱ��ǣ�������
A��B���ʵ�ͬʱ����ͬһ�㣬��ͬһ������ֱ���˶������˶���v-tͼ����ͼ��ʾ�������ʵ��ٴ�������ʱ��t��������ǰ����������s�ֱ��ǣ�������| A�� | t=8s��s=12m | B�� | t=8s��s=18m | C�� | t=4s��s=36m | D�� | t=8s��s=36m |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ����Ϊ1kg����龲ֹ��ˮƽ̨���ϵ�����ԭ�㣬���������Ķ�Ħ��������λ�ƵĹ�ϵ��ͼ����ʾ����������������ã��ɾ�ֹ��ʼ�����������������˶����˶���v-tͼ����ͼ����ʾ����3sĩǡ�õ���9mλ�ã�ȡ�������ٶ�g=10m/s2����
����Ϊ1kg����龲ֹ��ˮƽ̨���ϵ�����ԭ�㣬���������Ķ�Ħ��������λ�ƵĹ�ϵ��ͼ����ʾ����������������ã��ɾ�ֹ��ʼ�����������������˶����˶���v-tͼ����ͼ����ʾ����3sĩǡ�õ���9mλ�ã�ȡ�������ٶ�g=10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
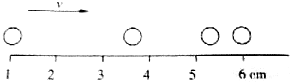 һС������������ֱ���˶�����Ƶ��������ĵ���Ƭ��ͼ��ʾ��Ƶ��������$\frac{1}{10}$s����С����ͼʾ�������˶���ƽ���ٶȴ�С�ǣ�������
һС������������ֱ���˶�����Ƶ��������ĵ���Ƭ��ͼ��ʾ��Ƶ��������$\frac{1}{10}$s����С����ͼʾ�������˶���ƽ���ٶȴ�С�ǣ�������| A�� | 0.25m/s | B�� | 0.2m/s | C�� | 0.17m/s | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����

| A�� | ͨ����Դ�ĵ������� | B�� | ����R�еĵ�����С | ||
| C�� | ���A���䰵һЩ | D�� | ���B���䰵һЩ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
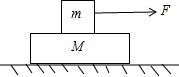 ��ͼ��ʾ������ΪM�ij�ľ��λ�ڹ⻬ˮƽ���ϣ�����Ϊm����龲ֹ�ڳ�ľ���ϣ������֮��Ļ���Ħ������Ϊ�̣��ֶ����mʩ��ˮƽ���ҵĺ���F��������Fʹ��ľ������������Ի����������F����СֵΪ���������ٶȴ�СΪg������볤ľ��֮������Ħ������������֮��Ļ���Ħ��������������
��ͼ��ʾ������ΪM�ij�ľ��λ�ڹ⻬ˮƽ���ϣ�����Ϊm����龲ֹ�ڳ�ľ���ϣ������֮��Ļ���Ħ������Ϊ�̣��ֶ����mʩ��ˮƽ���ҵĺ���F��������Fʹ��ľ������������Ի����������F����СֵΪ���������ٶȴ�СΪg������볤ľ��֮������Ħ������������֮��Ļ���Ħ��������������| A�� | ��mg��1+$\frac{m}{M}$�� | B�� | ��mg��1+$\frac{M}{m}$�� | C�� | ��mg | D�� | ��Mg |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
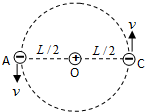 ��ͼ��ʾ��������Ϊm�ĵ���A��O��C��ɡ�����ϵͳ����λ��ͬһֱ���ϣ�����A��CΧ�Ƶ���O��ͬһ�뾶Ϊ$\frac{L}{2}$��Բ��������У�����A��C���������Ϊ-q������O���������Ϊ+q������������Ϊk����������֮��������������ã���������
��ͼ��ʾ��������Ϊm�ĵ���A��O��C��ɡ�����ϵͳ����λ��ͬһֱ���ϣ�����A��CΧ�Ƶ���O��ͬһ�뾶Ϊ$\frac{L}{2}$��Բ��������У�����A��C���������Ϊ-q������O���������Ϊ+q������������Ϊk����������֮��������������ã���������| A�� | ����A��C��Բ���˶������ٶȴ�Сv=$\sqrt{\frac{{2k{q^2}}}{mL}}$ | |
| B�� | ����A��C��Բ���˶��Ľ��ٶȦ�=$\sqrt{\frac{{6k{q^2}}}{{m{L^3}}}}$ | |
| C�� | ����A��C��Բ���˶�������T=$\sqrt{\frac{{2m{��^2}{L^3}}}{{3k{q^2}}}}$ | |
| D�� | ����A��C��Բ���˶��ļ��ٶ������ǵ������� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com