
 at2,得:
at2,得: aBt2-
aBt2- aAt2=L,
aAt2=L, mvA2+
mvA2+ MvB2 -
MvB2 - (M+m)v2,解得:Em=0.4J;
(M+m)v2,解得:Em=0.4J; mvA2+
mvA2+ MvB2=
MvB2= mvA′2+
mvA′2+ MvB′2,
MvB′2,

科目:高中物理 来源: 题型:
 如图所示,质量m=4.0kg的物体与地面的动摩擦因数μ=0.50,物体在与地面成θ=37°的恒力F作用下,由静止开始运动,运动0.20s撤去F,又经过0.40s物体刚好停下.(sin37°=0.60)求:
如图所示,质量m=4.0kg的物体与地面的动摩擦因数μ=0.50,物体在与地面成θ=37°的恒力F作用下,由静止开始运动,运动0.20s撤去F,又经过0.40s物体刚好停下.(sin37°=0.60)求:查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,质量M=4.0kg的长木板B静止在光滑的水平地面上,在其右端放一质量m=1.0kg的小滑块A(可视为质点).初始时刻,A、B分别以v0=2.0m/s向左、向右运动,最后A恰好没有滑离B板.已知A、B之间的动摩擦因数μ=0.40,取g=10m/s2.求:
如图所示,质量M=4.0kg的长木板B静止在光滑的水平地面上,在其右端放一质量m=1.0kg的小滑块A(可视为质点).初始时刻,A、B分别以v0=2.0m/s向左、向右运动,最后A恰好没有滑离B板.已知A、B之间的动摩擦因数μ=0.40,取g=10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:
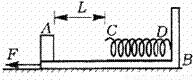
 (2011?重庆一模)如图所示,质量M=4.0kg的滑板B静止于光滑的水平面上.滑板右端固定着一根轻质弹簧,弹簧的自由端C到滑板左端的距离L=0.5m,在L=0.5m这一段滑板上B与木块A之间的动摩擦因数μ=0.2,而弹簧的自由端C到弹簧固定端D所对应的滑板上表面光滑.可视为质点的木块A质量m=1.0kg,静止于滑板的左端.滑板B受水平向左的恒力F=14.0N,作用一定时间后撤去该力,此时木块A恰好运动到滑板C处(g取10.0m/s2).试求:
(2011?重庆一模)如图所示,质量M=4.0kg的滑板B静止于光滑的水平面上.滑板右端固定着一根轻质弹簧,弹簧的自由端C到滑板左端的距离L=0.5m,在L=0.5m这一段滑板上B与木块A之间的动摩擦因数μ=0.2,而弹簧的自由端C到弹簧固定端D所对应的滑板上表面光滑.可视为质点的木块A质量m=1.0kg,静止于滑板的左端.滑板B受水平向左的恒力F=14.0N,作用一定时间后撤去该力,此时木块A恰好运动到滑板C处(g取10.0m/s2).试求:查看答案和解析>>
科目:高中物理 来源: 题型:
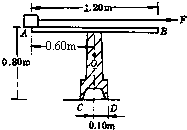 质量M=2.0kg的小铁块静止于水平轨道AB的A端.导轨及支架ABCD形状及尺寸如图所示,质量m=4.0kg.它只能绕通过支架D点垂直于纸面水平转动,其中心在图中的O点,现有一细线沿导轨拉小铁块,拉力F=12N,小铁块和导轨之间的动摩擦因数μ=0.50.g取10m/s2从小铁块运动时起,导轨(及支架)能保持静止的最长时间是多少?
质量M=2.0kg的小铁块静止于水平轨道AB的A端.导轨及支架ABCD形状及尺寸如图所示,质量m=4.0kg.它只能绕通过支架D点垂直于纸面水平转动,其中心在图中的O点,现有一细线沿导轨拉小铁块,拉力F=12N,小铁块和导轨之间的动摩擦因数μ=0.50.g取10m/s2从小铁块运动时起,导轨(及支架)能保持静止的最长时间是多少?查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,质量M=4.0kg,长L=4.0m的木板B静止在光滑水平地面上,木板右端与竖直墙壁之间距离为s=6.0m,其上表面正中央放置一个质量m=1.0kg的小滑块A,A与B之间的动摩擦因数μ=0.2.现用大小为F=18N的推力水平向右推B,两者发生相对滑动,作用1s后撤去推力F,通过计算可知,在B与墙壁碰撞时A没有滑离B.设B与墙壁碰撞时间极短,且无机械能损失,重力加速度g=10m/s2.求A在B上滑动的整个过程中,A,B系统因摩擦产生的内能增量.
如图所示,质量M=4.0kg,长L=4.0m的木板B静止在光滑水平地面上,木板右端与竖直墙壁之间距离为s=6.0m,其上表面正中央放置一个质量m=1.0kg的小滑块A,A与B之间的动摩擦因数μ=0.2.现用大小为F=18N的推力水平向右推B,两者发生相对滑动,作用1s后撤去推力F,通过计算可知,在B与墙壁碰撞时A没有滑离B.设B与墙壁碰撞时间极短,且无机械能损失,重力加速度g=10m/s2.求A在B上滑动的整个过程中,A,B系统因摩擦产生的内能增量.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com