
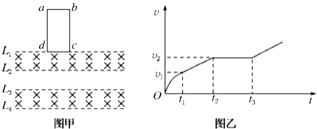
 ��ͼ����ʾ������ֱ�����������������ȵ�ˮƽ����L1��L2��L3��L4����L1L2֮�䡢L3L4֮�������ǿ�ų�����С��Ϊ1T������ֱ����������ƽ�森����һ������Ȧabcd������cd=L=0.5m������Ϊ0.1kg������Ϊ2���������ͼʾλ�þ�ֹ�ͷţ�cd����L1�غϣ����ٶ���ʱ��ı仯��ϵ��ͼ����ʾ��t1ʱ��cd����L2�غϣ�t2ʱ��ab����L3�غϣ�t3ʱ��ab����L4�غϣ���֪t1��t2��ʱ����Ϊ0.6s�������˶���������Ȧƽ��ʼ�մ�����ֱ�����������ٶ�gȡ10m/s2��������
��ͼ����ʾ������ֱ�����������������ȵ�ˮƽ����L1��L2��L3��L4����L1L2֮�䡢L3L4֮�������ǿ�ų�����С��Ϊ1T������ֱ����������ƽ�森����һ������Ȧabcd������cd=L=0.5m������Ϊ0.1kg������Ϊ2���������ͼʾλ�þ�ֹ�ͷţ�cd����L1�غϣ����ٶ���ʱ��ı仯��ϵ��ͼ����ʾ��t1ʱ��cd����L2�غϣ�t2ʱ��ab����L3�غϣ�t3ʱ��ab����L4�غϣ���֪t1��t2��ʱ����Ϊ0.6s�������˶���������Ȧƽ��ʼ�մ�����ֱ�����������ٶ�gȡ10m/s2��������| A�� | ��0��t1ʱ���ڣ�ͨ����Ȧ�ĵ����Ϊ0.25C | |
| B�� | ��Ȧ�����˶����ٶȴ�СΪ8m/s | |
| C�� | ��Ȧ�ij���Ϊ1m | |
| D�� | 0��t3ʱ���ڣ���Ȧ����������Ϊ4.2J |
���� ��1�����ݸ�Ӧ�����q=$\frac{����}{R}$�����������
��2��t2��t3���ʱ������Ȧ������ֱ���˶�����Ȧ���ܵİ�����������ƽ�⣬����ƽ���������ֱ���˶����ٶȣ�
��3��ͨ����Ȧ��t1��t2��ʱ�����ڣ�������Ȧ�Ĵ�ͨ��û�иı䣬û�и�Ӧ������������Ȧ���ȼ���ֱ���˶������ٶ�Ϊg��֪��cd��L2Ϊ��״̬����ab�߸ս�L3Ϊĩ״̬����ų��Ŀ���Ϊd������Ȧ�½���λ��Ϊ3d���������˶�ѧ��ʽ�����Ȧ�ij��ȣ�
��4�����������غ����0��t3���ʱ������Ȧ���������ĵ��ȣ�
��� �⣺B������ƽ���У�mg=BIL����I=$\frac{BLv}{R}$
������ʽ���v=$\frac{mgR}{{B}^{2}{L}^{2}}$=$\frac{1��2}{{1}^{2}��0��{5}^{2}}$m/s=8m/s����B��ȷ��
C��t1��t2��ʱ��������Ȧһֱ���ȼ���ֱ���˶���֪��cd��L2Ϊ��״̬����ab�߸ս�L3Ϊĩ״̬����ų��Ŀ���Ϊd������Ȧ�½���λ��Ϊ3d�����У�
3d=vt-$\frac{1}{2}$gt2��v=8m/s��t=0.6s��������d=1m��
������Ȧ�ij���ΪL��=2d=2m����C����
A����0��t1ʱ���ڣ�cd�ߴ�L1�˶���L2��ͨ����Ȧ�ĵ����Ϊq=$\frac{����}{R}$=$\frac{BLd}{R}$=$\frac{1��0.5��1}{2}$C=0.25C����A��ȷ��
D��0��t3ʱ���ڣ����������غ�ã�Q=mg��3d+2d��-$\frac{1}{2}$mv2=1����3��0.5��J=1.5J��
��ѡ��AB��
���� �������Ĺؼ�������Ȧ���˶������ѡ����ʵĹ��ɽ�����⣬������ѵ����ͨ����Ȧ�ȼ���ֱ���˶��ھ�������λ��Ϊ�ų����ȵ�3����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��
�� ������ȫ��ͬ������С���̵�������װ�ɵģ�
������ȫ��ͬ������С���̵�������װ�ɵģ� ��������5V��
��������5V�� ��������15V��Ϊ�˲���15--20V�ĵ�ѹ�����ǰ�
��������15V��Ϊ�˲���15--20V�ĵ�ѹ�����ǰ� ��
�� ��������ʹ�ã�����������ȷ���ǣ�������
��������ʹ�ã�����������ȷ���ǣ�������| A�� |  �� �� ��ʾ����� ��ʾ����� | |
| B�� |  �� �� ��ƫת�Ƕ���ͬ ��ƫת�Ƕ���ͬ | |
| C�� |  �� �� ��ʾ������ȣ�ָ��ƫת�Ƕ�Ҳ����ͬ ��ʾ������ȣ�ָ��ƫת�Ƕ�Ҳ����ͬ | |
| D�� |  �� �� ʾ��֮�ȵ�������ѹ��������֮�� ʾ��֮�ȵ�������ѹ��������֮�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | X1������ | B�� | X2�Ǧ����� | C�� | X3������ | D�� | X4�ǵ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ������ܶ����� | B�� | �����ѹǿ���� | ||
| C�� | ������ӵ�ƽ�����ܼ�С | D�� | ������ӵķ������ܱ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{n}$ | B�� | $\frac{1}{{n}^{2}}$ | C�� | n | D�� | n2 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{pq}$�� | B�� | $\sqrt{\frac{q}{p}}$�� | C�� | $\sqrt{\frac{p}{q}}$�� | D�� | $\sqrt{p{q}^{3}}$�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
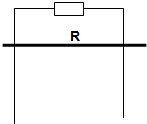 ��ͼ��ʾ������R=0.5������ֱ�����L=0.2m��������費�ƣ���һ����������m=0.01kg������r=0.5���������Ӵ����ã�����Ħ������ǿ�ų����������ƽ�洹ֱ���Ÿ�Ӧǿ��B=0.5T��g=10m/s2������������˶�ʱ���ٶȣ�
��ͼ��ʾ������R=0.5������ֱ�����L=0.2m��������費�ƣ���һ����������m=0.01kg������r=0.5���������Ӵ����ã�����Ħ������ǿ�ų����������ƽ�洹ֱ���Ÿ�Ӧǿ��B=0.5T��g=10m/s2������������˶�ʱ���ٶȣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com