
| A. | $\frac{R-d}{R+h}$ | B. | $\frac{(R-d)^{2}}{(R+h)^{2}}$ | C. | $\frac{(R-d)(R+h)^{2}}{{R}^{3}}$ | D. | $\frac{(R-d)(R+h)}{{R}^{2}}$ |
分析 根据题意知,地球表面的重力加速度等于半径为R的球体在表面产生的加速度,深度为d的地球内部的重力加速度相当于半径为R-d的球体在其表面产生的重力加速度,根据地球质量分布均匀得到加速度的表达式,再根据半径关系求解深度为d处的重力加速度与地面重力加速度的比值.卫星绕地球做圆周运动时,运用万有引力提供向心力可以解出高度为h处的加速度,再求其比值.
解答 解:令地球的密度为ρ,则在地球表面,重力和地球的万有引力大小相等,有:$g=\frac{GM}{R^2}$,
由于地球的质量为:$M=\frac{4}{3}π{R^3}ρ$,
所以重力加速度的表达式可写成:$g=\frac{4}{3}πGρR$.
根据题意有,质量分布均匀的球壳对壳内物体的引力为零,固在深度为d的地球内部,受到地球的万有引力即为半径等于(R-d)的球体在其表面产生的万有引力,故井底的重力加速度为:$g′=\frac{4}{3}πGρ(R-d)$,
所以有:$\frac{g′}{g}=\frac{R-d}{R}$.
根据万有引力提供向心力为:$G\frac{Mm}{{{{(R+h)}^2}}}=ma$,
“天宫一号”的加速度为:$a=\frac{GM}{{{{(R+h)}^2}}}$,
所以有:$\frac{a}{g}=\frac{R^2}{{{{(R+h)}^2}}}$,
得:$\frac{g′}{a}=\frac{{(R-d){{(R+h)}^2}}}{R^3}$,故C正确,ABD错误.
故选:C
点评 抓住在地球表面重力和万有引力相等,在地球内部,地球的重力和万有引力相等,要注意在地球内部距离地面d处所谓的地球的质量不是整个地球的质量而是半径为(R-d)的球体的质量m.


科目:高中物理 来源: 题型:解答题
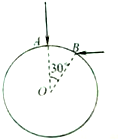 半径为R玻璃圆柱体,截面如图所示,圆心为O,在同一截面内,两束相 互垂直的同种单色光射向圆柱面的A、B两点,其中一束沿AO方向,∠AOB=30°,玻璃对此单色光的折射率n=$\sqrt{3}$,真空中光速为c.求:
半径为R玻璃圆柱体,截面如图所示,圆心为O,在同一截面内,两束相 互垂直的同种单色光射向圆柱面的A、B两点,其中一束沿AO方向,∠AOB=30°,玻璃对此单色光的折射率n=$\sqrt{3}$,真空中光速为c.求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 1g的0℃的水的内能比1g的O℃的冰的内能大 | |
| B. | 只要两物体的温度相同,它们的分子平均动能一定相同 | |
| C. | 阳光从缝隙射入教室,从阳光中看到的尘埃的运动是布朗运动 | |
| D. | 气缸里的气体难压缩说明了分子间有斥力 | |
| E. | 两分子间的引力和斥力都随它们的距离增大而减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 该卫星运行的向心加速度大小是地球表面重力加速度的$\frac{1}{{n}^{2}}$ | |
| B. | 该卫星运行的向心加速度大小是地球表面重力加速度的$\frac{1}{n}$ | |
| C. | 该卫星的运行速度大小是第一宇宙速度大小的$\frac{1}{{n}^{2}}$ | |
| D. | 该卫星的运行速度大小是第一宇宙速度大小的$\frac{1}{\sqrt{n}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
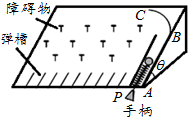 如图所示,是一儿童游戏机的工作示意图.游戏机的光滑面板与水平面成一夹角θ,半径为R的四分之一圆弧轨道BC与AB管道相切于B点,C点为圆弧轨道最高点,轻弹簧下端固定在AB管道的底端,上端系一轻绳,绳通过弹簧内部连一手柄P.将球投入AB管内,缓慢下拉手柄使弹簧被压缩,释放手柄,弹珠被弹出,与游戏面板内的障碍物发生一系列碰撞后落入弹槽里,根据入槽情况可以获得不同的奖励.假设所有轨道均光滑,忽略空气阻力,弹珠可视为质点.某次缓慢下拉手柄,使弹珠距B点为L,释放手柄,弹珠被弹出,到达C点时速度为v,下列说法正确的是( )
如图所示,是一儿童游戏机的工作示意图.游戏机的光滑面板与水平面成一夹角θ,半径为R的四分之一圆弧轨道BC与AB管道相切于B点,C点为圆弧轨道最高点,轻弹簧下端固定在AB管道的底端,上端系一轻绳,绳通过弹簧内部连一手柄P.将球投入AB管内,缓慢下拉手柄使弹簧被压缩,释放手柄,弹珠被弹出,与游戏面板内的障碍物发生一系列碰撞后落入弹槽里,根据入槽情况可以获得不同的奖励.假设所有轨道均光滑,忽略空气阻力,弹珠可视为质点.某次缓慢下拉手柄,使弹珠距B点为L,释放手柄,弹珠被弹出,到达C点时速度为v,下列说法正确的是( )| A. | 弹珠从释放手柄开始到触碰障碍物之前的过程中机械能守恒 | |
| B. | 此过程中,弹簧的最大弹性势能为mg(L+R) sinθ+$\frac{1}{2}$mv2 | |
| C. | 弹珠脱离弹簧的瞬间,其动能和重力势能之和达到最大 | |
| D. | 调整手柄的位置使L变化,可以使弹珠从C点离开后做匀变速直线运动,直到碰到障碍物 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 该卫星的向心加速度不变 | B. | 该卫星的线速度不变 | ||
| C. | 该卫星受到的合外力一定在变化 | D. | 该卫星的运动周期一定在变化 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
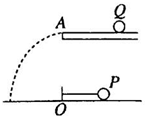 如图所示,小球P用长L=1m的细绳系着,在水平面内绕O点做匀速圆周运动,其角速度ω=2πrad/s.另一质量m=1kg的小球Q放在高出水平面h=0.8m的光滑水平槽上,槽口A点在O点正上方.当小球Q受到水平恒力F作用时,P球恰好在水平槽的正下方,水平槽与绳平行,Q运动到A时,力F自然取消(g取10m/s2).
如图所示,小球P用长L=1m的细绳系着,在水平面内绕O点做匀速圆周运动,其角速度ω=2πrad/s.另一质量m=1kg的小球Q放在高出水平面h=0.8m的光滑水平槽上,槽口A点在O点正上方.当小球Q受到水平恒力F作用时,P球恰好在水平槽的正下方,水平槽与绳平行,Q运动到A时,力F自然取消(g取10m/s2).查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,虚线a、b、c代表电场中的三个等势面,实线为一带正电的质点仅在电场力的作用下通过该区域时的运动轨迹,P、Q为质点先后通过电场时轨迹上的两个点,由此可知( )
如图所示,虚线a、b、c代表电场中的三个等势面,实线为一带正电的质点仅在电场力的作用下通过该区域时的运动轨迹,P、Q为质点先后通过电场时轨迹上的两个点,由此可知( )| A. | 三个等势面中,a的电势最高 | B. | 质点在Q点时,加速度较小 | ||
| C. | 质点通过P点时动能较大 | D. | 质点通过Q时电势能较小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com