
 ������ֱ���˶��������ٵ��ͷ�һ������ҲΪm��������Ϊ+q��q��0����С�����С���������룬�������ǡ��û�дӳ��ϵ�������
������ֱ���˶��������ٵ��ͷ�һ������ҲΪm��������Ϊ+q��q��0����С�����С���������룬�������ǡ��û�дӳ��ϵ�������
 =
= m
m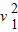 -
- ?2m
?2m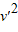
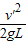 =0.5
=0.5 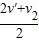 t-
t- t=
t=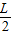
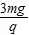
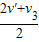 t-
t-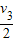 t=
t=
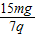
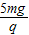
 ��E2��
��E2��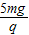 ��
�� ��
��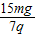 ��E2��
��E2�� ��
��

 ��ս100��Ԫ����Ծ�ϵ�д�
��ս100��Ԫ����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�
 ��2008?�Ƹ�ģ�⣩��ͼ��ʾ���ڹ⻬ˮƽ����ֱ��MN�Ҳ��д�ֱ��ˮƽ�����ǿ�ų���һ������ΪR�ľ����߿�abcd�ܵ�ˮƽ����ĺ㶨�������ã���һ���ij��ٶ����ҽ���ų�������һ��ʱ����������뿪�ų����������˶�������ab��ʼ��ƽ����MN�����߿������˶�����ų��������˶��뿪�ų������������У�������
��2008?�Ƹ�ģ�⣩��ͼ��ʾ���ڹ⻬ˮƽ����ֱ��MN�Ҳ��д�ֱ��ˮƽ�����ǿ�ų���һ������ΪR�ľ����߿�abcd�ܵ�ˮƽ����ĺ㶨�������ã���һ���ij��ٶ����ҽ���ų�������һ��ʱ����������뿪�ų����������˶�������ab��ʼ��ƽ����MN�����߿������˶�����ų��������˶��뿪�ų������������У��������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�
 ��ͼ��ʾ���ڹ⻬ˮƽ������ľ��A��B��mA=0.5kg��mB=0.4kg�����ǵ��ϱ����Ǵֲڵģ�����һС����C��mC=0.1kg���Գ���v0=20m/s����ľ����滬�������ͣ����B�ϣ���ʱB��C�Թ�ͬ�ٶ�v=3m/s�˶�����
��ͼ��ʾ���ڹ⻬ˮƽ������ľ��A��B��mA=0.5kg��mB=0.4kg�����ǵ��ϱ����Ǵֲڵģ�����һС����C��mC=0.1kg���Գ���v0=20m/s����ľ����滬�������ͣ����B�ϣ���ʱB��C�Թ�ͬ�ٶ�v=3m/s�˶������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�
 ��ͼ��ʾ���ڹ⻬ˮƽ���Ϸ��ų�ΪL������ΪM�ij�ľ�壬�ڳ�ľ����˷�һ����Ϊm����飨����Ϊ�ʵ㣩����ʼʱ����ͳ�ľ������ھ�ֹ״̬�����ͳ�ľ����Ǵֲڵģ�������mʩһˮƽ���ҵĺ���F�������ж���ȷ���ǣ�������
��ͼ��ʾ���ڹ⻬ˮƽ���Ϸ��ų�ΪL������ΪM�ij�ľ�壬�ڳ�ľ����˷�һ����Ϊm����飨����Ϊ�ʵ㣩����ʼʱ����ͳ�ľ������ھ�ֹ״̬�����ͳ�ľ����Ǵֲڵģ�������mʩһˮƽ���ҵĺ���F�������ж���ȷ���ǣ��������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�
 ��ͼ��ʾ���ڹ⻬ˮƽ���Ϸ�������Ϊ2kg�ij�ľ��B��ģ��B�Ҷ˾���ֱǽs=4m��ľ��B����һ����Ϊ1kg�Ľ�����A��������A��ľ��B�们��Ħ��������=0.20����ʼA�Ԧ�o=3m/s�ij��ٶ������˶���ľ��B�ܳ���A�����B�ϻ��£�ľ��B����ֱǽ��ײ������ǰ���ʷ��أ�����ײʱ�伫�̣�gȡ10m/s2����
��ͼ��ʾ���ڹ⻬ˮƽ���Ϸ�������Ϊ2kg�ij�ľ��B��ģ��B�Ҷ˾���ֱǽs=4m��ľ��B����һ����Ϊ1kg�Ľ�����A��������A��ľ��B�们��Ħ��������=0.20����ʼA�Ԧ�o=3m/s�ij��ٶ������˶���ľ��B�ܳ���A�����B�ϻ��£�ľ��B����ֱǽ��ײ������ǰ���ʷ��أ�����ײʱ�伫�̣�gȡ10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�
 ��ͼ��ʾ���ڹ⻬ˮƽ���Ͼ�ֹ��һ������ΪM=5kg�ij�����ľ��A��ľ�����˾�ֹ������һ����Ϊm=2kg�����B����֪AB֮�䶯Ħ��������=0.5������ʵ�鷢�ֵ������Bʩ��һ����СΪ16Nˮƽ���ҵ�����F��2s���B������ľ����Ҷˣ�gȡ10m/s2����
��ͼ��ʾ���ڹ⻬ˮƽ���Ͼ�ֹ��һ������ΪM=5kg�ij�����ľ��A��ľ�����˾�ֹ������һ����Ϊm=2kg�����B����֪AB֮�䶯Ħ��������=0.5������ʵ�鷢�ֵ������Bʩ��һ����СΪ16Nˮƽ���ҵ�����F��2s���B������ľ����Ҷˣ�gȡ10m/s2�����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com